Integral von ln kann mir jemand Lösung erklären?
Hallo allerseits! ich muss den integral von ln (x) berechnen, siehe angabe unten. die Lösung gibt an, den integral in zwei teile zu teilen... von 0 bis 1 und 1 bis e.. warum macht man das? und warum ist dann der ln teil von 0 bis 1 negativ, also warum nimmt man dann den integral von -ln?
Danke schonmal für eure Hilfe!!

5 Antworten
Hinweis:Grundregel bei der normalen Integration ist:Nicht über Nullstellen hinweg integrieren !
f(x)=ln(x) Nullstelle bei x=1
Bei der Integration erhält die Fläche unter der x-Achse und der Kurve ein negatives Vorzeichen und die Fläche über der x-Achse ein positives Vorzeichen
Gesamtfläche ist dann Ages=Aoben+Betrag A(unten)
Hier 2 Flächen A1 Integrationsgrenzen xu=0 bis xo=1
A2 Integrationsgrenzen xu=1 bis xo=e¹=e
Ausnahme bildet die Formel zur Berechnung einer Fläche zwischen 2 Kurven
A=Integral((f(x)-g(x))*dx)
Hier kann man über die Nullstellen hinweg integrieren,weil wegen -1*g(x) die Flächen unter der x-Achse ein positives Vorzeichen bekommen und deshalb automatisch zur Gesamtfläche Ages addiert werden.
f(x)=obere Begrenzung
g(x)=untere Begrenzung
Hinweis:Wenn die obere Begrenzung f(x) und die untere Begrenzung g(x)sich im Integrationsbereich abwechseln,dann führt das zu einen falschen Ergebnis.
Man muss dann den Integrationbereich in 2 Teile aufteilen,wo diese Abwechselung nicht stattfindet.
Das ist die Definition des Betrages.
|x|=x, wenn x>=0
|x|=-x, wenn x<0.
Analog ist dazu
|ln(x)|=ln(x), wenn ln(x)>=0
|ln(x)|=-ln(x), wenn ln(x)<0.
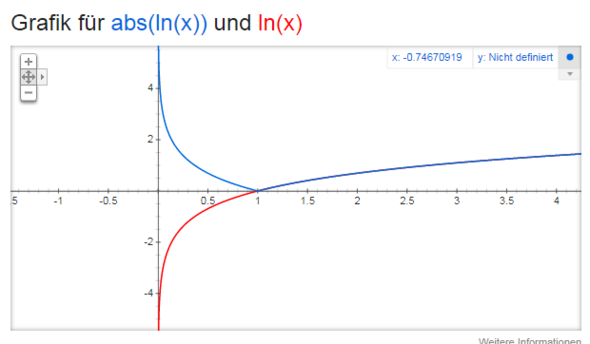
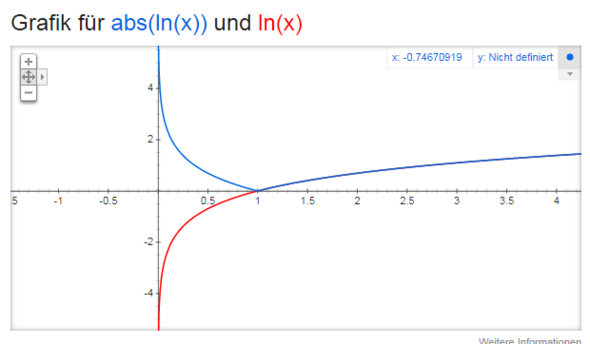
Nun besagt die Anmerkung über dem einen Gleichheitszeichen, dass ln(x)<0 für 0<x<1 gilt. Durch das Minuszeichen wird der ln für Werte zwischen 0 und 1 an der x-Achse gespiegelt, sodass er dort positiv ist.
siehe Mathe-Formelbuch,besondere Integrale
F(x)=Integral(ln(x)*dx)=x*ln(x)-x+C=x*(ln(x)-1)+C
Herleitung nach der partiellen Integration Integral(u*dv)=u*v-Integral(v*du
u=ln(x) du/dx=1/x ergibt du=dx/x
dv=dx integriert v=x
eingesetzt
F(x)=ln(x)*x-Integral(x*dx/x)=ln(x)*x-x+C
F(x)=x*(ln(x)-1)+C
ich muss den integral von ln (x) berechnen
Da dürfte das Problem liegen. Du sollst das Integral von |ln(x)| berechnen, nicht von ln(x). Nachdem der ln zwischen 0 und 1 negativ ist, wird dieser Integrationsbereich abgespalten, dort gilt nämlich |ln(x)| = -ln(x) (das ist größer Null), zwischen 1 und e hingegen gilt |ln(x)| = ln(x).
Hinweis: f(x)=ln(x) mit x<=0 nicht definiert Nullstelle bei x=1 weil ln(1)=0
e^0=1
0<x<1 ln(0,8)=-0,223..
x>1 Graph liegt oberhalb der x-Achse
0<x<1 Graph liegt unter der x-Achse