Energieniveaudiagramm von F_2?
Guten Tag,
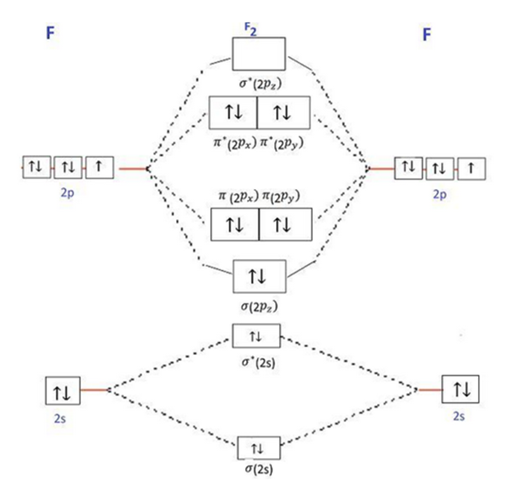
warum malt man in einem Energieniveaudiagramm zwei Kästchen für eine Pi-Bindung? Auch in eine Pi-Bindung passen doch nur zwei Elektronen.
F_2 hat eine Einfachbindung. Ich verstehe das so, dass es eine Einfachbindung ist, weil das bindende Sigma-2p-Orbital besetzt ist, das antibindende allerdings nicht. Kann man das so sagen, dass der fehlende Ausgleich für die Bindung sorgt? Mit anderen Worten: Wenn das antibindende Sigma-2p-Orbital besetzt wäre, würde keine F–F Bindung stattfinden, richtig?
Ich habe diese Erklärung angeschaut: https://www.youtube.com/watch?v=Iv_ECjUNcRs
Die 2p_y und 2p_z-Orbitale sind in dem Diagramm voll besetzt. Trotzdem binden sie nicht (ich vermute, dass das daran liegt, dass die antibindenden Orbitale ebenfalls besetzt sind (?)). Aber wo befinden sich diese Elektronen in der Lewis-Formel?
In der Lewis-Formel von F–F gibt es ja insgesamt sechs freie Elektronenpaare, d. h. 12 Valenzelektronen, die nicht an der Bindung beteiligt sind. Wo finde ich diese Elektronen im Energieniveaudiagramm? Ich nehme an, gar nicht (?). Warum zeichnet man dann die bindenden und nichtbindenden Pi-2p-Orbitale mit insgesamt acht Elektronen?
Ich verstehe die Elektronenkonfiguration von Fluor und auch von F_2, nur das Diagramm kann ich nicht verstehen.
Vielen Dank. :)
2 Antworten
Ich verstehe das so, dass es eine Einfachbindung ist, weil das bindende Sigma-2p-Orbital besetzt ist, das antibindende allerdings nicht. Kann man das so sagen, dass der fehlende Ausgleich für die Bindung sorgt? Mit anderen Worten: Wenn das antibindende Sigma-2p-Orbital besetzt wäre, würde keine F–F Bindung stattfinden, richtig?
Korrekt. So funktioniert das.
Zum zweiten Teil: Lewis-Formel und MO-Diagramm sind zwei paar Schuhe, die kann man nicht vergleichen. Das eine ist ein Formalismus zum Zeichnen von einfach Strukturformeln, das andere ist ein Diagramm zur Visualisierung von Quantenchemischen Rechnungen.
Formal sind die nicht-bindenden bzw. freien Elektronenpaare der Lewis-Formel die Elektronepaare im σ2s, σ*2s, den beiden π und π* Orbitalen. Die sind in der Lewis-Formel alle äquivalent, im MO-Diagramm aber offensichtlich nicht. D.h. du kannst das MO-Diagramm nicht so ohne weiteres auf eine Lewis-Formel übertragen und umgekehrt auch nicht. Die Lewis-Formel ist eben nur ein Formalismus und keine getreue Wiedergabe der realen Bindungssituation
Das wären zwei π-Bindungen (eine pro Kästchen). Denn du hast ja pro Fluor Atom je zwei p-Orbitale die überlappen können. Einmal die pz Orbitale miteinander und einmal die py Orbitale. Macht insgesamt 2 π-Bindungen, die ja aber von den anti-π-Bindungen wieder aufgehoben werden
Danke! px- und py-Orbitale können aber allein von der Anordnung her gar keine Bindung eingehen, oder verstehe ich das falsch?
Doch natürlich. Wenn sie auf der Bindungsachse liegen wird eine σ Bindung draus. Wenn sie senkrecht dazu stehen, eine π-Bindung.
Siehe hier. Die oberen beiden sind σ Bindungen, die unteren π Bindungen
Natürlich können zwei p-Orbitale eine Bindung eingehen; ich meinte, ob ein px und ein py orbital eine Bindung eingehen können
Ach so, ja das macht keinen Unterschied. Die drei p Orbitale sind entartet, also energetisch gleichwertig und ununterscheidbar.
Trotzdem binden sie nicht (ich vermute, dass das daran liegt, dass die antibindenden Orbitale ebenfalls besetzt sind (?)).
Du vermutest richtig. In diesem einfachen Bild ergibt sich die Doppelbindung einfach aus der Differenz der besetzten bindenden und antibindenden Orbitale — es sind vier bindende Orbitale besetzt (2 σ und ein π, das entartet ist und daher doppelt zu zählen ist), und drei antibindende (σ und π). Schnell aus dem Internet geklaut:

Obwohl dieses Bild unglaublich vereinfacht ist, kannst Du daraus trotzdem ein paar richtige Schlüsse ziehen: Z.B., wenn Du das F₂⁺-Ion ansiehst, erwartest Du eine stärkere (also auch kürzere) Bindung als im F₂, nämlich eine 1½-fache Bindung, weil das entfernte Elektron aus einem antibindenden Orbital genommen wird. Umgekehrt wirst Du bei F₂¯ entsprechend eine schwächere FF-Bindung erwarten, weil das Extra-Elektron in ein antibindendes Orbital geht.
Jetzt kommen wir zur etwas schwierigeren Frage: In diesem Diagramm gibt es bindende und antibindende Orbitale, aber keine nichtbindenden. Wo kommen dann die 6 nichtbindenden Elektronenpaare in der Lewis-Formel her?
Die Antwort ist, daß diese einsamen Elektronenpaare in diesem Fall sozusagen eine alternative Schreibweise für ein Paar aus bindenden und antibindenden Orbitalen darstellen. Für das tiefste Orbitalpaar können wir ja anschreiben σ(s)=s₁+s₂ und σ*(s)=s₁−s₂ (positive und negative Linearkombination der 2s-Orbitale). Daraus folgt aber umgekehrt, daß s₁=σ+σ* und s₂=σ−σ* (ohne Normierung), und diese ±-Linearkombinationen der MOs sind wieder die AOs und lassen sich als lone pair interpretieren, weil sie an einem einzigen Atom hängen.
- Warum in der Welt sollte man das machen? Die Antwort ist: Weil es egal ist, die Wellenfunktion und alle daraus berechneten Eigenschaften bleiben dieselben, wenn man die durch Linearkombinationen gebildeten MOs wieder zu den AOs zurückauflöst, solange man dabei nur doppelt besetzte Orbitale verwendet. Nobler gesagt: Die Wellenfunktion und damit alle berechneten Eigenschaften sind invariant auf orthogonale Transformationen im Unterraum der besetzten Orbitale.
- Das hat natürlich damit zu tun, daß Orbitale keine physikalische Bedeutung haben; sie sind nur Zwischengrößen auf dem Weg zur Gesamtwellenfunktion, die wirklich etwas Physikalisches beschreibt. Die kanonischen MOs haben ihre Vorteile, besonderes, wenn man Spektroskopie betreibt, weil man dann vieles aus der Form und Symmetrie der Orbitale qualitativ ableiten kann, ohne das man noch mehr rechnen muß (z.B. UV-Auswahlregeln, Koopmans Theorem).
- Andererseits sind sie aber auch unbequem, weil jedes MO im allgemeinen Fall übers ganze Molekül delokalisiert ist. Wenn es bequem ist, dann kann man sie auch wieder „lokalisieren“, also durch geeignete Linearkombinationen wieder auf ein Atom oder auf eine Bindung beschränken. Solange man nur besetzte Orbitale zu dieser Fummelei heranzieht, ist das in Ordnung.
- Beachte, daß man durch die Lokalisierung ein paar Eigenschaften verliert, z.B. haben die lokalisierten „MOs“ keine definierte Orbitalenergie mehr — das klingt aber schlimmer als es ist, denn erstens sind Orbitalenergien ohnehin nicht meßbar (Koopmans Theorem ist nur eine Näherung und stimmt zwar oft passabel, kann aber auch beliebig falsch sein), und zweitens ist die meßbare Gesamtenergie sowieso ungleich der Summe der einzelnen Orbitalenergien, auch wenn das komisch klingt.
- Durch die Lokalisierung verliert man also gewissen intuitive Anschauung (z.B. das jedes Elektron eine bestimmte Energie hat, was real nicht stimmt aber oft qualitativ gute Veranschaulichung bietet), und gewinnt andere (z.B. daß das nichtbindende Elektron an einem Atom hängt und nicht am anderen, obwohl das auch nicht stimmt). Man verliert auch alle Aussagen über Symmetrie, und kann deshalb mit lokalisierten Orbitalen keine qualitativen Aussagen über Spektroskopie oder Reaktivität (Woodward-Hoffman) machen.
- Im Fall des F₂ kann man die lone pairs durch Linearkombinationen σ₁, σ₁*, π und π* genau so bauen, daß sie der naiven Vorstellung von sp³-Hybridorbitalen entsprechen. Für viele Chemiker ist das eine gute Anschauung, also kann man es so machen und sagen „Jedes F-Atom hat drei gleichartige lone pairs“. Das ist eine mögliche Interpretation der Wellenfunktion (gleichwertig zur kanonischen mit delokalisirten σ,σ*,π,π*), aber halt nicht die einzig mögliche.
- Ein anderes Beispiel: Wenn Du z.B. H₂O hernimmst, dann bekommst Du zwei OH-bindende Orbitale, aber beide beschreiben beide Bindungen (einmal mit gleicher Phase und einmal mit verschiedener, also einem Knoten durchs O-Atom). Ihre Summe und Differenz entspricht lokalisierten Bindungen, und wenn man will darf man es sich so vorstellen. Die lokalisierte Beschreibung ist qualitativ gut, wenn man z.B. eine OH-Bindung zerreißen will, die delokalisierte ist qualitativ gut, wenn man z.B. UV-Spektroskopie verstehen will. Um echte, zum Experiment korrelierende Zahlen auszurechnen, braucht man sowieso viel mehr als nur Energieniveaux.
- Nochmals: Orbitale und ihre Energien beschreiben nichts Reales, nur die Gesamtelektronendichte ist real, und man kann aus vielen verschiedenen Sätzen von besetzten Orbitalen dieselbe Dichte bekommen.
- Es gibt aber auch Fälle, in denen eine solche Lokalisierung nicht möglich ist; wenn man es versucht, dann fällt man mathematisch auf die Nase. In einem solchen Fall muß man mit der delokalisierten Beschreibung leben. Beispiel Benzol.
- Auch im MO-Diagramm kann es nichtbindende Orbitale geben, z.B. beim NH₃: es gibt drei besetzte NH-bindende Orbitale (eines davon entartet), ein besetztes nichtbindendes am N und drei unbesetzte antibindende.
Wow, vielen Dank für die ausführlichen Erläuterungen. Ich habe jetzt auch verstanden, wieso eine Pi-Bindung zwei Kästchen braucht. Ich habe noch eine Nachfrage: Ein px- und ein py-Orbital können allein von der Anordnung her doch gar keine Bindung eingehen, oder?
Ja, die stehen aufeinander orthogonal und können daher in diesem Molekül nichts miteinander machen. In komplizierten Molekülen könnte man sich aber Geometrien ausdenken, in denen eine Bindung möglich ist, z.B. in einem Vierring, der wie ein Karo schräg im Koordinatensystem liegt.
Das habe ich jetzt viel besser verstanden, danke! Mich irritiert allerdings immer noch, wieso man zwei Kästchen mit insgesamt bis zu vier Elektronen für eine Pi-Bindung zeichnet. Oder verstehe ich das falsch?