Dynamik Physik Aufgabe: Wann kippt die Kiste?
Hallo Leute,
ich verzweifele gerade bei folgender Dynamik Aufgabe, die ich im Zuge meines Selbststudiums lösen wollte:
Ein fahrender LKW ist mit einer Kiste beladen. Die Höhe der Kiste beträgt 2 m, die Grundfläche 0,8 m x 0,8 m. Sie hat eine Masse von 1 t, ihr Schwerpunkt liegt in der Körpermitte. Berechnen Sie die Verzögerung des Lastwagens, bei der die Kiste zu kippen beginnt, wenn sie durch flache Klötze gegen Verschieben gesichert ist.
Mir ist überhaupt nicht klar, was ich mit der Höhe und der Fläche der Kiste anfangen soll. Also klar weiß ich die Gewichtskraft und somit auch die Normalkraft, aber weiter komme ich nicht.
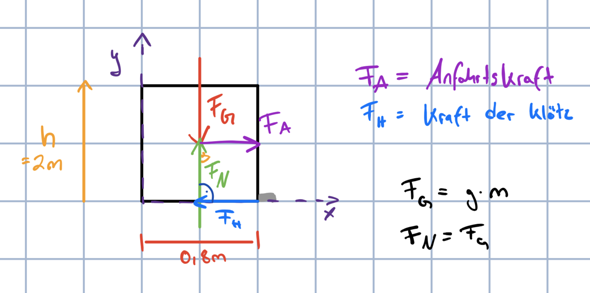
Hier noch meine Skizze, wobei ich mir bei der Positionierung von FA (Die Kraft die durchs anfahren erzeugt wird) nicht sicher bin.
4 Antworten
Das einzige, was man wissen muss, ist dass die Kiste genau dann anfängt zu kippen, wenn die Resultierende aus Gewichts- und Trägheitskraft auf den Eckpunkt der Kiste zeigt.
Der Rest ist reine Geometrie.
Durch die Beschleunigung (Verzögerung) entsteht ein Vektor (Kräftedreieck) aus Gravitation und Beschleunigung. Wenn der Vektor außerhalb dem Eckpunkt verläuft, kippt die Kiste. Anstelle der Kräfte kannst du die Beschleunigungen zeichnen. Die Masse ist unerheblich. Die Kiste kippt immer gleich, unabhängig vom Gewicht.
Der Rechenweg, für alle Interessierten.
Lösung war vorgegeben, somit sollte es richtig sein, solange der Prof keinen Fehler gemacht hat ;)
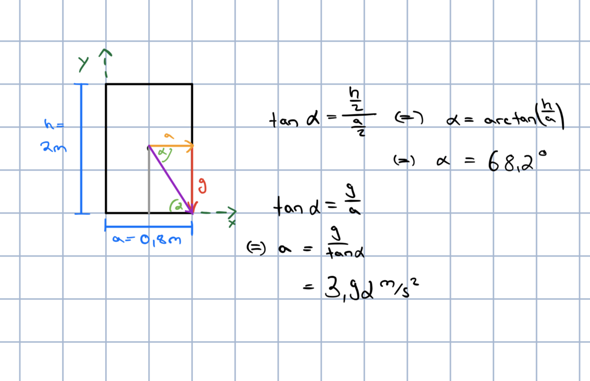
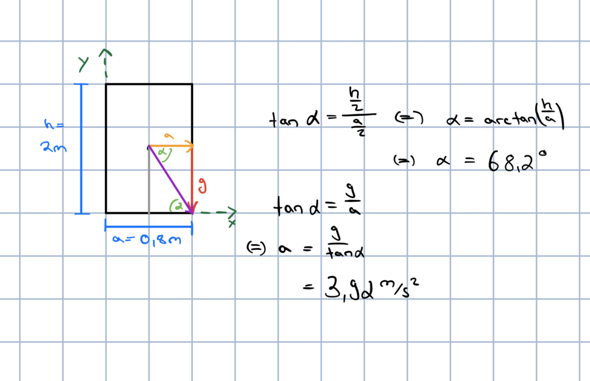
FA*1,0>FG*0,4... dann hebt die Kiste ab.
FG=m*g
FA=m*a... wobei a hier die gesuchte Bremsverzögerung ist