Maximale Höhe der Kraft F damit Schrank nicht kippt?
Ich habe eine Aufgabe bei dem ein Schrank auf einen schiefen Ebene steht. Die Ebene hat eine Steigung von 10°
Der Schrank wiegt 50 Kg, ist 2m hoch und 1m breit. Der Reibungskoeffizient my beträgt 0,2. Der Schwerpunkt ist genau in der Mitte
Der Schrank wird die Schräge hinaufgeschoben und es soll die maximale höhe h berechnet werden, an der die Kraft F wirken darf ohne das der Schrank kippt. Also das er lediglich geschoben wird.
Falls notwendig habe ich noch die Normalkraft FN = 483,04N, die Hangabtriebskraft FH= 85,17 und die Reibkraft FR 96,61N berechnet.
1 Antwort
Ich sehe keine Frage. Du hast nur die Aufgabe genannt. Wo kommst du denn genau nicht weiter?
Zudem gehört zu soetwas natürlich immer erst eine Skizze!
Diese habe ich mal gemacht.
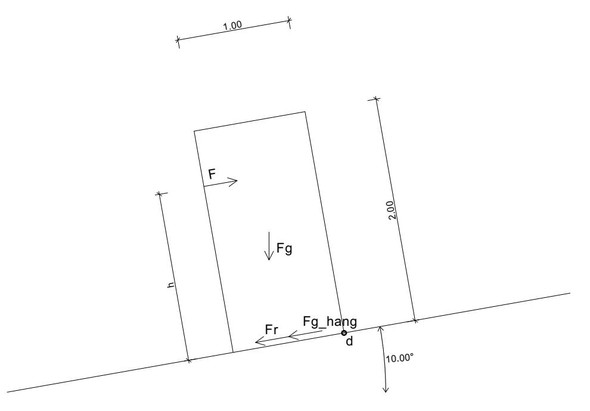
Damit der Schrank sich nach oben bewegen kann muss
F > Fr + Fg_hang
sein.
Damit er jedoch dabei nicht kippt, muss das Kippmoment kleiner sein als das Standmoment.
also F * h < Fg * (Abstand Fg zu d) = Fg_normal * 0,5 m
Da die Ungleichungen unpraktisch sind, könnte man auch Gleichheitszeichen einsetzen. Dann ermittelt man den theoretisch möglichen Punkt bei der theoretisch ausreichenden Kraft.
In der Praxis muss man dann tiefer anfassen, da man nicht unendlich langsam schieben will.
ja dann setzt doch einfach ein:
F > Fr + Fg_hang
181,8 N > 96,61 N + 85,17 N
181,8 N > 181,78 N
Bedingung erfüllt, die Kraft F würde (gerade so) ausreichen um den Schrank zu schieben.
Vorausgesetzt natürlich die Kraft ist so definiert wie in der Skizze gezeigt: Parallel zur Oberfläche der Ebene.
Also noch die 2. Ungleichung
F * h < Fg_normal * 0,5 m
nach h umstellen
h < Fg_normal * 0,5 m / F
Fg-normal ist die Normalkraft
F ist die Kraft mit der geschoben wird
muss man also nur noch 2 Zahlen einsetzen um h zu berechnen.
So habe ich mir das auch gedacht, habe aber meinen Prof gefragt und er sagte die richtige lösung ist 1,797m. Bei deiner Rechnung komme ich auf 1,328m.
Du hast recht, ich hatte den Anteil von Fr_hang übersehen.
Diese wirkt ja ebenfalls im Schwerpunkt und nicht wie in der Skizze auf der Ebene. Somit hat diese Kraft einen Abstand zum Drehpunkt d von 1,0 m.
F * h < Fg_normal * 0,5 m + Fg_hang * 1,0 m
h < (Fg_normal * 0,5 m + Fg_hang * 1,0 m) / F
h < (483,04 N * 0,5 m + 85,17 N * 1,0 m) / 181,8 N
h < 326,69 Nm / 181,8 N
h < 1,797 m
Danke für die Skizze und die Antwort. Ich habe da wohl ne kleingkeit vergessen :D.
Die Kraft mit der gedrückt wird beträgt: 181,8 N.
Die Frage ist: Berechnen Sie die maximale Höhe der Kraft F, wenn der Schrank beim Anschieben rutschen und nicht kippen soll!