Das A-t Diagramm richtig auswerten?
Hallo liebe Community :) Heute hab ich eine Frage zu Physik, bzw. zum Beschleunigung Zeit Diagramm. Ich hab mir schon Gedanken gemacht und es versucht aber dennoch wollte ich nochmal nachfragen.
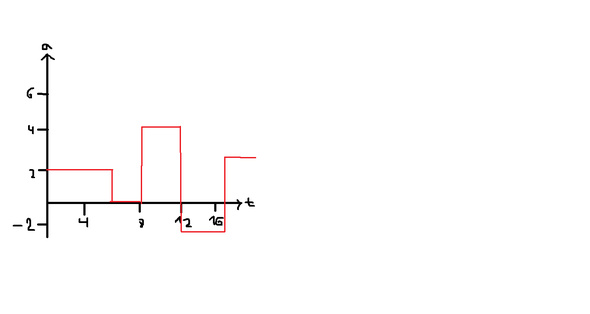
Das folgende Diagramm zeigt, eine gleichmäßige beschleunigte Bewegung. Ich weiß auch, dass wenn a= parallel zur t-achse ist, konstant ist. Problem: Wie soll ich die Geschwindigkeit bzw, die Strecke hier ablesen können.
Also ist v in den ersten 6s-- 2m/s^2 6 ? =12 m/s und dann ist v=0 ? später 8s -- 8s4m/s^2 ?
Danke im Vorraus :)
2 Antworten
Also wir haben auf der x-Achse t und auf der y-Achse a
Für die Geschwindigkeit gilt:
v = a * t
oder ∆v = a * ∆t
Damit entspricht die Geschwindigkeitsänderung der Fläche, die durch t1, t2, der Kurve und der x-Achse eingeschlossen wird.
Im Diagramm sind 5 Phasen eingezeichnet:
1. Phase: ∆v1 = 2 m/s^2 * 6s = 12 m/s
v1 = v0 + ∆v1 = 12 m/s (bei v0 = 0)
2. Phase: ∆v2 = 0 m/s^2 * 4s = 0 m/s
v2 = v1 + ∆v2 = 12 m/s
3. Phase: ∆v3 = 4 m/s^2 * 4s = 16 m/s
v3 = v2 + ∆v3 = 28 m/s
4. Phase: ∆v4 = -2 m/s^2 * 5s = -10 m/s
v4 = v3 + ∆v4 = 18 m/s
5. Phase: ∆v5 = 3 m/s^2 * 4s = 12 m/s
v5 = v4 + ∆v5 = 30 m/s
Wenn wir von v0 = 0 m/s ausgehen, ist die Endgeschwindigeit ve die Summe aller ∆v's
Also: ve = ∆v1 + ∆v2 + ∆v3 + ∆v4 + ∆v5 = 30 m/s
Streckenberechnung:
s = v * t
Das gilt aber nur bei konstanter Geschwindigkeit.
Bei einer gleichförmig beschleunigten Bewegung kann man mit der mittleren Geschwindigkeit vm rechnen.
vm = (v2 - v1) / 2 = ∆v /2
Damit ergibt sich:
1. Phase: ∆s1 = v0 * t1 + ∆v1 / 2 * t1 = 36 m
s1 = s0 + ∆s1
2. Phase: ∆s2 = v1 * t2 + ∆v2 / 2 * t2 =
s2 = s1 + ∆s2
3. Phase: ∆s3 = v2 * t3 + ∆v3 / 2 * t3 =
s3 = s2 + ∆s3
etc.
Bei der Streckenberechnung muss man die Anfangsgeschwindigkeit der Phase + die Änderung der Geschwindigkeit innerhalb der Phase berücksichtigen. Die Anfangsgeschwindigkeit einer Phase ist gleich der Endgeschwindigkeit der vorausgehenden Phase.
In jedem Zeitintervall, in denen die Beschleunigung konstant
ist, wird die Geschwindigkeitsänderung berechnet: Δv = a · Δt
Im ersten Zeitintervall lautet die Rechnung:
Δv = 2m/s · (6s - 0s) = 12m/s
Im zweiten Zeitintervall ist die Beschleunigung a = 0, d.h., dass sich in diesem Zeitintervall die Geschwindigkeit v nicht ändert: v = konst. = 12m/s.
etc.
Gruß, H.
Δv = 16m/s. Dieser Wert wird zu v = 12m/s addiert, so dass zum Zeitpunkt t = 12s die Geschwindigkeit v = 28m/s beträgt.
Also wäre beim nächsten Abschnitt, 8s-12s , also 4s * 4m/s^2 =16 m/s ?