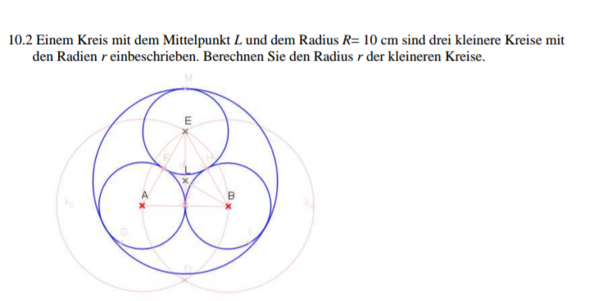
Berechnen Sie den Radius r der kleineren Kreise ?
Hallo , ich hoffe ,dass es euch gut geht ....... ich hab diese Frage (siehe Bild ). Kann jemand mir die Lösung oder den Lösungsweg geben ? Danke im voraus,,,
8 Antworten
Hierbei ist folgender mathematischer Satz wichtig:
Die Seitenhalbierenden (Höhen) eines gleichseitigen Dreiecks schneiden sich im Verhältnis 2:1.
Sei R der Radius des großen Kreises, h eine beliebige Höhe des gleichseitigen Dreiecks und r der Radius der kleinen Kreise, so gilt:
R = 2/3 * h + r
Denke dir nun ein rechtwinkliges Dreieck, dessen Hypotenuse die Strecke BL, also 2/3 * h ist. Dessen Katheten sind somit r und 1/3 * h.
Mit dem Satz des Pythagoras lässt sich folgende Gleichung aufstellen:
(1/3 * h)² + r² = (2/3 * h)²
Durch Äquivalenzumformungen ergibt sich:
r = √((2/3 * h)² - (1/3 * h)²)
= √(4/9 * h² - 1/9 * h²)
= √(3/9 * h²)
= √(1/3 * h²)
= √(1/3) * h
= 1/√3 * h
= h/√3
Damit hast du deine zweite Gleichung, mithilfe der du nun ein lineares Gleichungssystem mit zwei Variablen aufstellen kannst:
I 10 = 2/3 * h + r
II r = h/√3
II' r * √3 = h
II' in I:
10 = 2/3 * r * √3 + r | Distributivgesetz
10 = r * (2/3 * √3 + 1) | :(2/3 * √3 + 1)
r = 10/(2/3 * √3 + 1) ≈ 4,64
Der Radius der kleinen Kreise beträgt also etwa 4,64 cm. ^^
Ich hoffe, ich konnte dir helfen; wenn du noch Fragen hast oder einen Schritt nicht nachvollziehen konntest, kommentiere einfach, damit ich dir helfen kann. ;)
LG Willibergi
Hallo,
der Radius r des kleinen Kreises beträgt 4,641 cm.
Begründung:
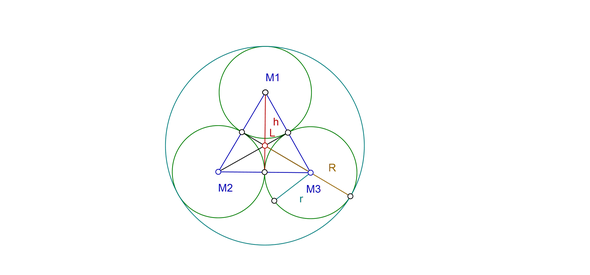
Gehe von dem gleichseitigen Dreieck aus. Jede Seite dieses Dreiecks ist gleich 2r. Der Mittelpunkt des Dreiecks liegt auf der Höhe h (rot). Seine Höhe über der Basis ist (1/3)*h, weil sich die Seitenhalbierenden eines Dreiecks im Verhältnis 1:2 schneiden.
h²=4r²-r²=3r²
h=r*√3
Die Strecke LH ist dann r/√3
(LM3)²=r²+r²/3=4r²/3
LM3=(2r)/√3
R=LM3+r=r+(2r)/√3=10
(√3r+2r)/3=10
r*(√3+2)=10*√3
r=(10*√3)/(√3+2)=4,641
Siehe Skizze
Herzliche Grüße,
Willy
Hi, Beniceman,
mal der Versuch eines kurzen Weges.
Die Strecke vom Mittelpunkt zum Rand des großen Kreises ist 10 cm, vom Mittelpunkt zu einem der Dreieckpunkte des gleichseitigen Dreiecks 10-r.
Der Winkel zwischen dieser Strecke und der Dreiecksseiten ist 30 °, die Dreiecksseiten betragen 2r.
Der Winkel gegenüber der Grundseite (2r) und der beiden Strecken 5-r beträgt 120°.
Nun kann man einfach den Sinussatz anwenden.
2r/sin(120°) = (10-r)/sin(30°).
Nach r umstellen, fertig.Ohne Taschenrechner: irgendwie zwischen 4 und 5.
Ich denke, mit Hilfe der Skizze sollte dieser weg nachvollziehbar sein.
Der Radius der kleineren Kreise müsste bei ungefähr 4,6 cm liegen. Wie man das allerdings berechnet, würde mich auch interessieren.
Es muss irgendwie auf trigonometrische Weise gehen.
Gut geschätzt! (oder nachgemessen ^^)
Auf trigonometrische Weise ist das imho nicht möglich, da lediglich die Winkel des gleichseitigen Dreiecks gegeben sind, wobei sich beim Aufstellen einer Gleichung die Variablen in allen Fällen wegkürzen und eine wahre Aussage entstehen müsste. ;)
LG Willibergi
Geht hier mit Handy schlecht, daher nur die Idee: Der Mittelpunkt im gleichseitigen Dreieck teilt die Höhen im Verhältnis 2/3 zu 1/3. Also ist 2/3 • h + r = R, wobei r der Radius des kleinen und R der Radius des großen Kreises ist. h = 2r /2 • √3. Einsetzen und nach r auflösen, fertig.