Gleichgewichtskonstant?

Säure + Alkohol ⟶ Ester + Wasser

Der Umsatz soll unter irgendwelchen Bedingungen 70% betragen, wenn man die bei­den Edukte äquimolar mischt, aus einem Mol Edukt werden also 0.7 mol Produkt, und 0.3 mol Edukt bleiben übrig. Das setzen wir ins Massenwirkungsgesetz ein und rech­nen es einfach aus:

Dabei habe ich das MWG ausnahmesweise direkt mit Stoffmengen, nicht Konzentra­ti­onen formuliert. Das kann ich in diesem Fall machen, weil sich die Teilchenzahl nicht ändert.

In der zweiten Frage soll berechnet werden, wieviel Alkohol man braucht, um die Aus­beute (bezogen auf die Carbonsäure) auf η=95% zu steigern.

• Nenne den gefragten Überschuß r, also n₀(Alkohol)=r⋅n₀(Säure). Die tiefgestellte Null zeigt dabei an, daß das Einwaagemengen sind, nicht die Mengen im Gleich­gewicht. Nennen wir die Einwaagemenge an Säure einfacherweise n₀.
• Im Gleichgewicht sollen η=95% der Säure zu Ester und Wasser reagiert haben, also n(Ester)=n(Wasser)=ηn₀.
• Umgekehrt bleiben im Gleichgewicht 5% der Carbonsäure übrig, also n(Säure)=(1−η)n₀.
• Zuletzt stellt sich die Frage nach dem Alkohol. Wir beginnen mit der Stoffmenge rn₀, und 95% von n₀ reagieren, also bleiben rn₀−ηn₀=(r−η)n₀ übrig.

Also kennen wir alle vier Gleichgewichtskonzentrationen. Wir können nun ins Massen­wirkungs­gesetz gehen und nach r auflösen:

Damit haben wir also die Antwort: Wir brauchen den 4.27-fachen Ethanolüberschuß.

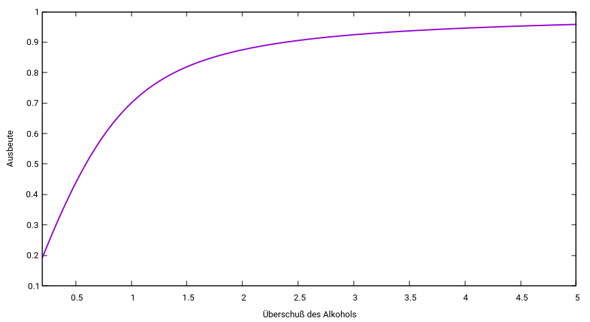
Wir können aber noch eine kleine Fleißaufgabe machen: Dazu lösen wir uns das Mas­sen­wirkungs­gesetz nicht nach r, sondern nach η auf. Dann erhalten wir eine quadra­tische Gleichung, und deren Lösung gibt an, wie die Ausbeute mit der eingesetz­ten Alkoholmenge zusammenhängt. Sinnvollerweise plotten wir das dann:

Man sieht, daß in diesem die Ausbeutesteigerung zemlich moderat bleibt. Von den 75% bei r=1 (äquimolar) geht es nur langsam bergauf, zu 95% bei r=4.27. Man ver­schwen­det also ziemlich viel Alkohol für ziemlich wenig Estergewinn.

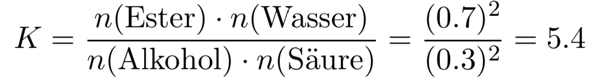
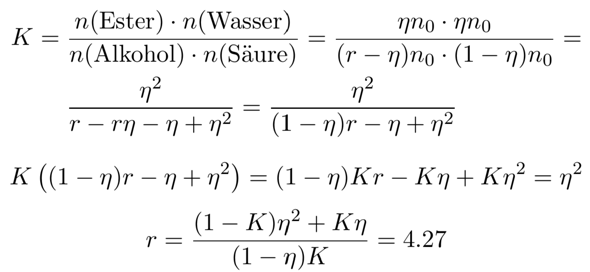
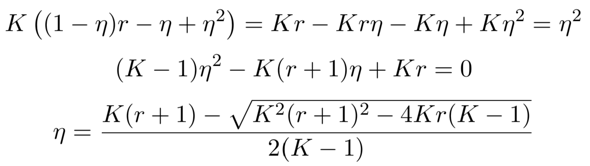
a) K = 70 * 70/(30 * 30) = 5,44

b) 1

Was ist für b) geschrieben habe, ist wegen meiner Verständnisprobleme beim Lesen der Aufgabe natürlich Müll. Daher noch einmal ganz langsam.

Da es hier um relative Konzentrations- bzw. Stoffmengenverhältnisse geht, setze ich den Ausgangswert für die Carbonsäure einfach gleich 1.

c(S₀) = 1

Die Einheiten können wir schlabbern, da sich diese ohnehin rauskürzen.

Die Säure reagiert zu 95 % zum Ester und zu Wasser. Damit gilt am Gleichgewichtspunkt:

c(E) = c(H₂O) = 0,95

Übrig bleibt am Gleichgewicht also der unreagierte Anteil der Carbonsäure:

c(S) = c(S₀) - 0,95 = 0,05

Die Alkoholkonzentration am Gleichgewicht nenne ich x. Dann ergibt sich für das Massenwirkungsgesetz:

5,44 = 0,95 * 0,95/(0,05 * x)

x = 3,34

0,95 vom Alkohol sind nach der Reaktion im Ester gebunden, sodass die Ausgangskonzentration des Alkohols

c(A₀) = 3,34 + 0,95 = 4,29

betragen muss.

Bezogen auf 1 für die Carbonsäure ist das ein Überschussverhältnis von 4,29.