Woher kommt 2k(Pi)?(Komplexe Zahlen)?
Hi
Meine Aufgabe lautet:
Welche komplexen Zahlen erfüllen die Gleichung (z +i)^3 =(i−1)^6 ? Verwenden Sie die Formel von Moivre und geben Sie die Lösungen sowohl in der algebraischen als auch in der exponentiellen Form an.
Die Lösung ist im Bild zu sehen.
Wie komme ich denn auf die 2k(Pi) die im Bild rot gekennzeichnet sind. Manchmal sind es ja auch nur ein Pi oder?
Dankeschön!

1 Antwort
Hallo ChemieHeld,
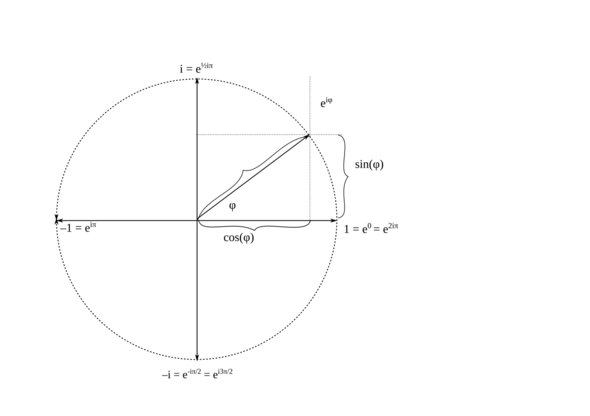
die Funktion
e^{iφ} = cos(φ) + isin(φ)
ist 2π - periodisch, d.h., es ist genau dann
e^{iφ + 2kπi} = e^{iφ},
wenn k eine Ganze Zahl ist. Deshalb kann man im Exponenten 2kπi mit einer beliebigen Ganze Zahl addieren, ohne etwas zu verändern.
Woher ich das weiß:Studium / Ausbildung