Wir haben aktuell das Thema "Satz des Pythagoras" und ich komme bei der Aufgabe leider nicht weiter. Vielleicht kann mir jemand helfen?
Ich hoffe, jemand kann mir helfen und erklären, wie ich zu der Lösung komme.

2 Antworten
Du hast:
Hypotenuse: Seite gegenüber vom rechten Winkel
Zwei katheten: die anderen Seiten
Die allgemeine Formel lautet:
a² + b² = c²
Hierbei sind a und b die katheten und c ist die Hypotenuse.
Jetzt setzt du nur deine angegebenen Buchstaben für katheten und Hypotenuse ein.
Bei b also: c² + b² = a²
Dann setzte du dafür die Werte ein:
6² + b²= 10²
Du möchtest immer den Wert, welchen du herausfinden möchtest alleine stehen haben. In dem Fall musst du die Rechnung also noch umformen. Also nimmst du den Wert minus welcher die Zahl ist.
Dann steht da: b²= 10² - 6²
Jetzt nur noch die Wurzel ziehen und fertig!

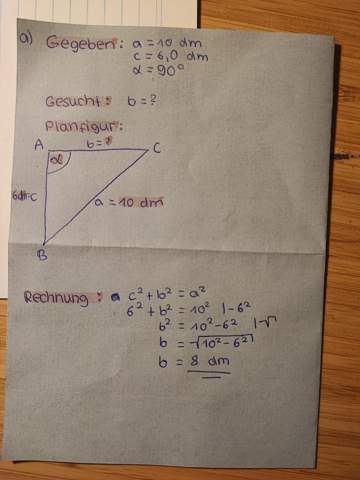
Die Winkelangabe zeigt, welche Seite Hypotenuse ist. Also ist bei a) die Seite a die Hypotenuse.
Also b² + c² = a².
In Dezimetern:
b² + 6² = 10²
Also b = 8.
Bei b) ist Beta der rechte Winkel, also ist b die Hypotenuse. (Zumindest bei den üblichen Bezeichnungen am Dreieck.)
Die Aufgaben c) und d) sind etwas schwieriger, weil hier der Flächeninhalt A gegeben ist.
Bei d) z.B. ist a die Hypotenuse und b und c sind die Katheten.
Weil A = b * c / 2 ist, kann man aus A und b erstmal c ausrechnen und über a² = b² + c² dann auch a.
Ich hatte bei Aufgabe B irgendwie c als Hypotenuse und bin auf 14,43 Meter gekommen. Ist das grundsätzlich falsch?
Wenn c die Hypotenuse wäre, dann wäre das richtig.
Aber weil b die Hypotenuse ist, ist das falsch. Beta ist 90° und die Hypotenuse liegt immer dem rechten Winkel gegenüber.
Wäre das richtige Ergebnis dann Hypotenuse B = 14,43 Meter?
Nein. Die Hypotenuse ist gegeben: b = 12 m.
Gesucht ist die Kathete c mit b² = a² + c². (oder c² = b² - a²)
Ach so, ich glaube, ich habe es jetzt verstanden.
a = 8 Meter (Kathete)
b = 12 Meter (Hypotenuse)
c = 14,43 Meter (Kathete)
b ist die Hypotenuse, weil sie dem Winkel Beta gegenüberliegt.
Stimmt das so?
Vielen Dank! :)
Was wäre denn dann das Ergebnis für Aufgabe 2, also was wäre dort c?