Wie rechnet man 64=2^x?
Würde gerne wissen wie das geht. Wir hatten das noch nicht in der Schule aber würde es gerne verstehen. Ich weiß, dass die Lösung 6 ist, aber wie kommt man drauf?
Vielleicht kennt ihr ja ein YouTube Video in dem das erklärt wird oder ihr könnt es einem Realschüler 10. Klasse erklären . Ich habe kein YouTube Video gefunden.
Wie heißt das Thema eigentlich?
Danke das reicht. Hätte nicht gedacht, dass ich so mit Antworten erschlagen werde!!! Der Begriff Logarithmus hat mir gefehlt.
13 Antworten
Dabei musst du einen Logarithmus benutzen. Dazu gibt es sicherlich viele Videos auf Youtube. Ansonsten guck nach exponentiellen Funktionen.
Hier habe ich eine sehr kurze Lösung für dein Beispiel hinzugefügt, den Logarithmus berechnet man mit dem Taschenrechner.
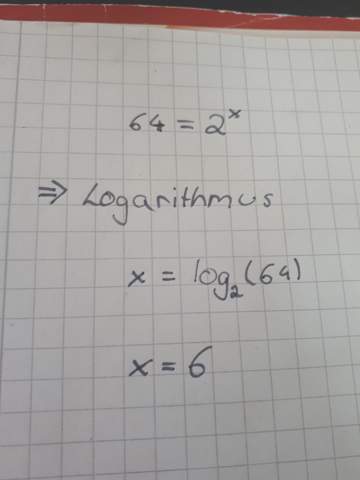

Dies ist eine Logarithmusaufgabe.
Dabei wird der Exponent (hier x) bestimmt, also wird geguckt, mit welcher Zahl man die Basis (hier 2) potenzieren muss, damit das Ergebnis (hier 64) rauskommt.
64 = 2^x | log
log2(64)=6
x=6
Das kannst du mit deinem Taschenrechner lösen.
Du kannst die 64 in eine 2er-Potenz umwandeln: 64=2⁶, d. h. 2⁶=2^x.
Sind bei 2 Potenzen die Basen gleich, dann müssen auch die Exponenten gleich sein.
Kommt das mal nicht hin z.B. 63=2^x, dann musst Du den Logarithmus anwenden...
63=2^x |logarithmieren (log, ln, lb, ...)
log(63)=log(2^x) |Logarithmusregel anwenden: log(a^b)=b * log(a)
log(63)=x * log(2) |: log(2)
log(63)/log(2)=x
Nur so kann es ein Realschüler 10 Klasse, verstehen. Logarythmen kennen die nicht.
Wir mussten "damals" (80er) in der 9. Klasse mit Logarithmustafeln den log bestimmen - HORROR. Habe ich jetzt noch Alpträume von :)
Dachte mittlerweile wären, dank Taschenrechner, kompliziertere Exponentialgleichungen im Lehrplan, daher auch mein weiteres Beispiel...
Hierfür muss man den Logarithmus verwenden. Man kann die Gleichung dann so umschreiben:
64=2^x
x=log(64) zur Basis 2
Das gibt man dann in den Taschenrechner ein und dann kommt
x=6
raus.
2^(x)=64 logarithmiert
ln(2^(x)=x*ln(2)=ln(64) siehe Mathe-Formelbuch,Logarithmengesetz log(a^(x))=x*log(a)
x=ln(64)/ln(2)=6
Oder mit dem Logarithmus mit der Basis 10
x=log(64)/log(2)=6
ln(64)=ln(2^(x))=x*ln(2)
x=ln(64)/ln(2)=6
oder x=log(64)/log(2)=6
Hinweis:Der Logarithmus mit der Basis 2 ist nicht auf den Rechner installiert.