Hallo liebe Community,
ich habe folgende Aufgabe:
Finden Sie alle a Element R, so dass die Vektoren
in R^3 linear abhängig sind.
Ich bin da nun wie folgt rangegangen. Ich habe mir erstmal ein Gleichungssystem erstellt um a auszurechnen:
Dieses Gleichungssystem habe ich mit Taschenrechner gelöst und kam auf
Ein weiteres Ergebnis war, dass a eine beliebige Zahl sein kann, aber dies ist nur der Fall, wenn Lambda1, Lambda2 und Lambda3 null sind und das soll ja hier nicht sein, da damit die lineare Abhängigkeit nicht gezeigt ist. Die lineare Abhängigkeit ist ja durch eine nicht-triviale Linearkombination = 0 gezeigt. Aber wenn alle Lambdas 0 wären, dann wäre es ja eine triviale Linearkombination.
Es wäre nett wenn mir jemand einen Ansatz geben könnte wie ich dieses Gleichungssystem auch händisch löse, weil ich kriege das nur mit Taschenrechner hin.
Ich habe probiert die erste Gleichung nach Lambda1 aufzulösen und das Ergebnis davon dann in die anderen Gleichungen einzusetzen kam damit aber nicht wirklich weit. Was ich durch meine Rechnung mit Taschenrechner schon weiß ist, dass für Lambda2 eigentlich wieder Lambda2 rauskommen sollte, aber ich weiß nicht wie man damit dann auf die Plus/Minus Wurzel 3 kommt. Ich habe auch probiert die erste Gleichung nach a aufzulösen, kam aber auch damit nicht wirklich weit.
Aber das händische Ausrechnen des Gleichungssystems ist eher Nebensache, aber es wäre trotzdem cool, wenn mir jemand einen Ansatz dafür geben könnte. Wir sollen die Aufgabe in einem Behauptung-Beweis-Schema aufschreiben und wir müssen keinen Rechenweg angeben. Also war meine Idee jetzt als Behauptung folgendes zu schreiben:
Für a = +-sqrt(3) Element der reellen Zahlen sind die Vektoren (1 a 0), (a 1 2) und (0 1 -1) in R^3 linear abhängig.
Um nun diese Behauptung zu beweisen bin ich wie folgt vorgegangen. Ich habe dieses Gleichungssystem aufgestellt:
Und bin damit auf folgende Lösungen gekommen:
Lambda 3 ist eine beliebige reelle Zahl, ungleich 0. Da es für a = sqrt(3) eine nicht-triviale Linearkombination gibt die den Wert null annimmt, sind die Vektoren (1 a 0), (a 1 2), (0 1 -1) linear abhängig für a = sqrt(3).
Das gleiche mache ich dann noch für a = -sqrt(3) und dann habe ich ja damit meine Behauptung bewiesen und somit auch die Aufgabe gelöst, oder?
Habe ich alles richtig gemacht? Wo ich mir nicht ganz sicher bin ist, halt, dass ich nirgendwo zeige, dass +-sqrt(3) die einzigen beiden Möglichkeiten für a sind so dass die Vektoren linear abhängig sind.
Also habe ich alles richtig gerechnet, richtig gedacht und habe ich die Beweisführung richtig gemacht? Oder denkt ihr ich sollte die Behauptung ändern in:
a = +-sqrt(3) sind die einzigen beiden Möglichkeiten für a sodass die Vektoren ... linear abhängig sind.
Und dann würde ich in meinen Beweis noch die Berechnung von a einbauen.
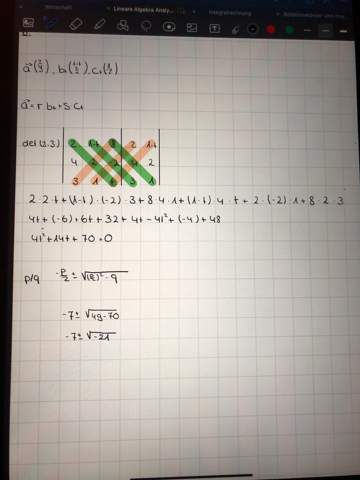

Habe ich gemacht, nur kommt bei mir dann eine ungültige Lösung (habe es mit der p/q Formel gemacht)