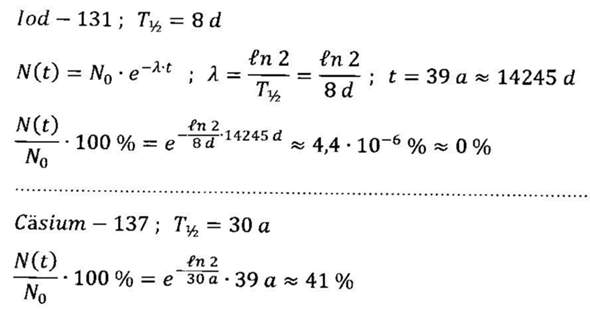Wie löse ich dieses Beispiel?

Man braucht den natürlichen log dafür aber ich weiß nicht wie ich das aufstelle.

Answer 1

[Peppie85]

um die genaue Anzahl an Tagen zu ermitteln hilft Excel.

für jeden Tag ab dem 1. Januar 1900, welcher dem Wert 0 entspricht hat Excel einen Wert.

wenn wir nun die genaue Uhrzeit des Unfalles eingeben, und dann in eine weitere Zelle "jetzt()" dann kommen, stand 03.05.2025, 14:27 also eine Differenz von 14.256 Tagen, bzw. was etwa 39,06 Jahren entspricht oder 342.085 Stunden heraus.

das bedeutet, dass sich die Menge an Cäsium etwa 1,3 mal halbiert hat die Menge an Jod 475,12 mal.

Du rehcnest jetzt jeweils 0,5 hoch 1,41 halbzeiten, dabei kommen etwa 38% heraus.

mit den rund 475 Halbzeiten kommt dabei eine derart kleine Zahl heraus, dass man schon nicht mehr von existent reden kann. Angesichts der hintergrundstrahlung vernachlässigbar.

Answer 2

[mihisu]

Da braucht man keinen Logarithmus dafür.

Wenn zu Beginn N₀ Kerne des entsprechenden Isotops vorhanden gewesen sind und diese mit einer Halbwertszeit von T zerfallen, so sind von diesen Kernen nach einer Zeit t noch N(t) Kerne übrig, wobei gilt...

$N(t)=N_0\cdot \left(\frac{1}{2}\right)^{\frac{t}{T}}$

Für den Anteil der N(t) noch vorhandenen Kerne in Bezug zur ursprünglichen Kernanzahl N₀ erhält man dann dementsprechend...

$\frac{N(t)}{N_0}=\left(\frac{1}{2}\right)^{\frac{t}{T}}$

Und da musst du dann die gegebenen Werte einsetzen, und das Ergebnis noch in Prozent umrechnen. Eine Umrechnung in Prozent kann man beispielsweise durch Multiplikation mit 100 % erreichen. Also...

$\frac{N(t)}{N_0}=\left(\frac{1}{2}\right)^{\frac{t}{T}}\cdot 100\,\%$

Vom 26. April 1986 bis heute (3. Mai 2025) sind 14252 Tage bzw. etwa 39,02 Jahre vergangen. [Da der 3. Mai nicht allzu weit vom 26. April entfernt ist, könnte man auch einfach mit ungefähr 39 Jahren rechnen.]

$t\approx 14252\,\text{d}\quad \text{ bzw. }\quad t\approx 39\text{,}02\,\text{a}$

============

Bei Teilaufgabe a) erhält man dann...

$\frac{N(t)}{N_0}=\left(\frac{1}{2}\right)^{\frac{t}{T}}\cdot 100\,\%\approx \left(\frac{1}{2}\right)^{\frac{14252\,\text{d}}{8\,\text{d}}}\cdot 100\,\%\approx 5\text{,}2\cdot {10}^{-535}\,\%$

Das sind, wenn man es ausschreibt...

0,00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000052 %

Da es im gesamten sichtbaren Universum weniger als 10^100 Atome (übliche Schätzungen liegen bei etwa 10^80 als Größenordnung) gibt, kann man demnach erwarten, dass keiner der ursprünglichen Iod-131-Kerne noch vorhanden ist, da man rechnerisch auf deutlich weniger als einen verbleibenden Kern kommt.

============

Bei Teilaufgabe b) erhält man dann...

$\frac{N(t)}{N_0}=\left(\frac{1}{2}\right)^{\frac{t}{T}}\cdot 100\,\%\approx \left(\frac{1}{2}\right)^{\frac{39\text{,}02\,\text{a}}{30\,\text{a}}}\cdot 100\,\%\approx 40\text{,}6\,\%$

Comments

[Flo0406]

Dankeschön 🙏

Answer 3

[Halswirbelstrom]

LG H.