Wie hoch ist die Wahrscheinlichkeit mit n Würfeln eine höhere Augenzahl zu werfen als mit n+1 Würfeln?
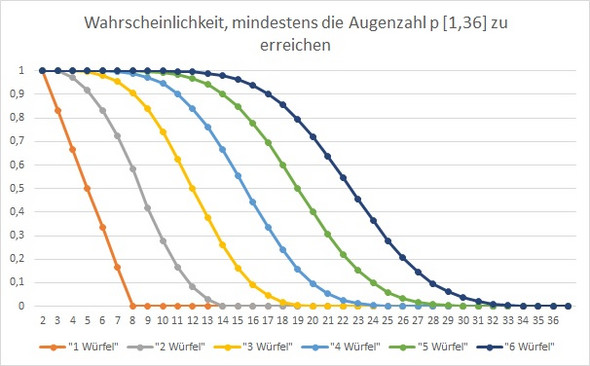
Ich habe bereits in Excel mithilfe von http://mathworld.wolfram.com/Dice.html ausgerechnet, wie hoch die Wahrscheinlichkeit ist, mit n Würfeln (hier 1 bis 6) mindestens die Augenzahl p (von 1 bis 36) zu erreichen, siehe Anhang. Die Wahrscheinlichkeiten können vorausgesetzt werden.
An dieser Stelle hänge ich aber. Ich dachte zuerst an die Differenz der Graphen, z.B. (1&2) und dann eine Summe über p. Aber dann wäre die Wslk, mit einem kleineren n eine größere Augenzahl zu würfeln immer 0 (oder kleiner 0). In der Realität geht das natürlich.
Hat jemand eine Idee zu diesem Gedankenexperiment?
2 Antworten
Scheint mir ein eher komplexes Problem zu sein.
Xn sei die Augensumme aus n unabhängigen Würfen
Xn+1 sei die Augensumme aus n+1 unabhängigen Würfen, die auch von den ersten n Würfen für Xn unabhängig sein sollen
Wir suchen P( Xn+1 < Xn )
Das kann man schreiben als
Summe( k= n+1 bis 6(n+1) ) P( Xn+1= k ) P( k < Xn )
Auf mathworld ĥast du die Formel für P( Xn+1= k ) gesehen, auch P( k < Xn ) kann man damit berechnen. Aber schön ist das nicht.
Wie wär's mit einer Monte Carlo Simulation? Geht sogar in Excel, zwei Spalten abfüllen, die erste mit der Summe aus n+1 Würfen, die zweite mit der Summe aus n Würfen, vergleichen, 10'000 Zeilen, vielleicht auch mehr, "Treffer" zählen.
Was mir noch einfällt, man kann auch eine Normalapproximation machen wie in mathworld angedeutet.
Y = Xn+1 - Xn hat den Erwartungswert 3.5 und die Varianz ( 2n+1 ) * 3.5
Wir suchen dann Phi( 0, mu= 3.5, sigma= Wurzel( ( 2n+1 ) * 3.5 ), kumuliert ) oder auf die Standardnormalverteilung skaliert
Phi( -3.5 / Wurzel( ( 2n+1 ) * 3.5 ) )
Die Varianz bei einem Wurf ist 3.5, und addiert sich bei unabhängigen Würfen. Und man würfelt ja n+1 + n mal, um Y = Xn+1 -Xn zu ermitteln.
Phi ist die Normalverteilung, in Excel wäre das NORMVERT.
Ich habe das Problem jetzt mal simuliert, wie eterneladam vorgeschlagen hat. Ist natürlich keine analytische Lösung, aber zumindest ein Anhaltspunkt.. (gemittelt wurde über 20000 Runden)
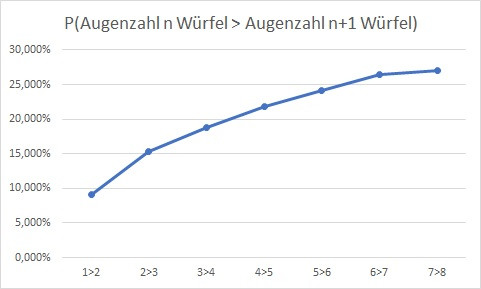
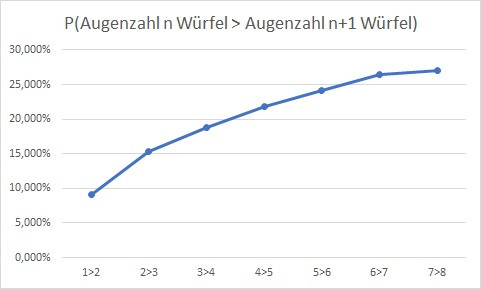
Schön, gerne auch noch für grössere Anzahl Würfel :-)
Für die Anzahl gegen unendlich würde ich einen Grenzwert von 0.5 vermuten, weil der eine Würfel mehr dann keinen Unterschied mehr machen sollte.
Danke für deine Antwort. Ich denke die Definition von P( Xn+1 < Xn ) ist schon mal hilfreich :)
Die Idee mit der Normalverteilung ist auch gut. Wenn ich deinen Kommentar richtig verstehe, suchen wir schließlich P(Y)? Ist das gleichbedeutend wie P( Xn+1 < Xn ) von oben? Das wäre dann ja ein schöner Ansatz.
Den E{Y}=3.5 kann ich noch nachvollziehen, die Varianz dann leider nicht mehr. Und beim Phi, was meinst du genau damit?