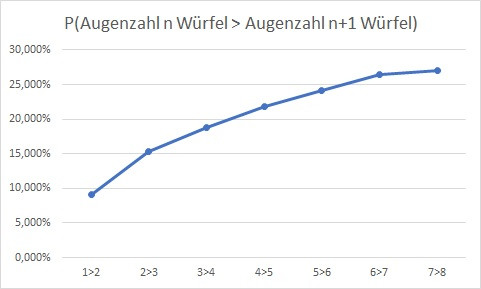
Ich habe das Problem jetzt mal simuliert, wie eterneladam vorgeschlagen hat. Ist natürlich keine analytische Lösung, aber zumindest ein Anhaltspunkt.. (gemittelt wurde über 20000 Runden)
Also z.B. beim ersten:
0,034cm² = ? mm²
cm -> mm (Umrechnungsfaktor: 10)
Du hast hier aber immer Flächen gegeben, cm² oder mm². 1mm² = 1mm * 1mm. Daher musst du den Umrechnungsfaktor hoch 2 nehmen, also im ersten Bsp. 10² = 100.
0,034cm² = 3,4 mm²
Zum Überprüfen: Wenn du in eine kleinere Einheit umrechnest, muss der Zahlenwert größer werden :)
Jetzt bist du dran :)
Also man könnte die Aufgabe einfach mit einer Formel berechnen, aber ihr sollt das wahrscheinlich gerade lernen, also machen wirs Schritt für Schritt, mithilfe von dem Bild :)
Die erste Zeile h^2 = kannst du mit der Angabe noch berechnen, richtig?
Was bedeutet das Ergebnis grafisch, das du herausbekommst?
...Genau, es ist die Fläche des Quadrats mit der Seitenlänge h (großes Quadrat).
Nächste Zeile: a^2/4. Was soll das?
Ich behaupte, das ist der Flächeninhalt des kleinen Quadrates unten rechts. Warum? Weil (a/2)*(a/2) = a^2/4 ist, und die Seitenlänge des kleinen Quadrats halb so groß ist wie die vom Dreieck. Nämlich genau a/2!
Okay, also die zweite Zeile weißt du im Moment noch nicht. Aber wenn du aufs Bild schaust, siest du, dass wenn du die Fläche des großen Quadrats durch vier teilst, dann hast du das kleine..
Also kannst du nun die Fläche des kleinen Quadrats angeben?
Das Ergebnis kommt in die zweite Zeile!
Bis hierhin alles klar?
Dichte = Masse / Volumen (kg/(dm)^3).
Das ist die Grundformel, die man sich merken muss.
Gesucht ist die Länge, also eine Größe, mit der man das Volumen berechnen kann.
Also Formel nach Volumen umstellen:
Volumen = Masse / Dichte
Masse ist gegeben. Dichte nehm ich an auch. (8,9 Kilogramm pro Kubikdezimeter)
Also probiere mal, das Volumen auszurechnen.
Wenn du das Volumen hast, kannst du mit der Formel:
Volumen = 20 mm * 100 mm * Länge
die Länge ausrechnen.
Also ich würde den Nenner zunächst umschreiben, und das j in den Exponenten stellen. j ist ja e^j90°. Also zusammen: 3*e^(j*150°)
Jetzt kannst du den Nenner mit der Euler'schen Formel umrechnen:
3*e^(j*150°) = 3*(cos (150°) + sin(150°))=3*(-sqrt(3)/2+ j*0,5)
So, jetzt nimmst du den Bruch und diesen Nenner, und erweiterst komplex konjugiert. Also mit 3*(-sqrt(3)/2- j*0,5).
Dann wirst du sehen, dass im Nenner keine komplexe Zahl mehr steht. Somit kannst du Real- und Imaginärteil getrennt angeben!
Dichte = Masse/Volumen (erkennst du an der Einheit kg/(dm)^3)
Umstellen nach Masse: Masse = Dichte * Volumen.
Also musst zu zunächst das Volumen berechnen:
Vollzylinder: r^2*pi*Länge
also: (0,05 dm)^2*pi*1000 dm = 7,85 (dm)^3
Minus "Luftloch": (0,02 dm)*(0,02 dm)*1000 dm = 0,4 (dm)^3
-> Volumen = 7,45 (dm)^3
Masse = 7,45 (dm)^3 * 8,9 kg/(dm)^3 = 66,3 kg.
Wichtig: Immer die gleichen "Einheiten" miteinander verrechnen!
Hier steht (dm)^3 für Kubikdezimeter.