Wie gibt man die passende Potenzfunktion an?

Hallo Leute,

Ich habe in Mathe die Aufgabe, dass ich den Term einer passenden Potenzfunktion angeben soll. Der Graph muss den Punkt P(-2|16) enthalten. Bei der zweiten Aufgabe muss der Graph symmetrisch zum Ursprung sein und den Punkt P(0,5|32) beinhalten.

Wie genau löst man solche Arten von Aufgaben und wie kommt man auf den richtigen Ansatz?

Answer 1

[verreisterNutzer]

Potenzfunktion ist so definiert:

$f\left(x\right)=a\cdot x^n\ \ \ a\ \in\mathbb{R},\ a\ne0,\ n\ \in\mathbb{N}\ \ \left(oder\ n\in\mathbb{R}\right)$

Es gibt also 2 Unbekannte a und n und damit wird das mit einem einzigen Punkt nichts weiter werden, denn um 2 Unbekannte zu bestimmen benötigt man - wie schon bei der Bestimmung einer Geradengleichung - auch 2 Punkte oder weitere Zusatzinformationen.

Gelöst wird das durch Verwerten der Informationen in Form von Gleichungen, die die Unbekannten enthalten. Das ergibt dann ein Gleichungssystem, das es zu lösen gilt und dann hat man a und n.

Aufgabe a) P(-2|16)

$f\left(-2\right)\ =a\cdot\left(-2\right)^n=16\ \to\ \left(-2\right)^n=\frac{16}{a}$

Ich würde mir -- da es keine weitere Information gibt, das Leben leicht machen und a=1 vorgeben und dann

$\left(-2\right)^n=16\ \to n\ =\ 4$

schreiben - daher wäre eine mögliche Potenzfunktion (es gäbe viele andere):

$f\left(x\right)=x^4$

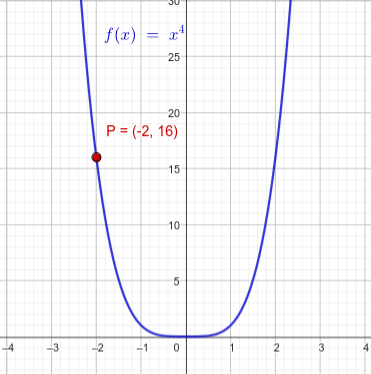
Skizze:

Tipp zur 2. Aufgabe:

Die Formulierung "Bei der zweiten Aufgabe muss der Graph symmetrisch zum Ursprung sein" heißt, dass der Exponent ungerade sein muss und wenn man jetzt ganz schlau sein möchte, dann legt man eine Ursprungsgerade durch den Punkt P (eine Gerade ohne Achsenabschnitt ist eine Potenzfunktion mit n = 1 und a = Steigung der Geraden)

Answer 2

[Halbrecht]

eine Potenzfunktion hat die Form 

f(x) = ax^n

.

man kann nun ein n wählen

einfachst : : : : : n = 2 , die Parabel

f(x) = a*x²

Punkt

16 = a*(-2)²

4 = a 

.

Aber auch n = 7 

16 = a*(-2)^7

16/(-2)^7 = a

.

Es gibt also nicht DIE richtige Antwort.

.

Symmetrisch zum Ursprung sind alle f(x) mit ungeradem Exponenten