Wie breit ist der Fluss?
„ ein Turm ist d= 8m von einem gradlinig verlaufendem Fluss entfernt. Von der Aussichtsplattform in 20m Höhe erscheint das jenseitige Flussufer unter einem Winkel von alpha= 50 Grad. Wie breit ist der Fluss?
könnt ihr mir bitte helfen? Ich versteh das nicht ganz und brauche darum eine Lösung ( ich lerne ein wenig Mathe in den Ferien)
anbei ein Foto von der Aufgabenstellung:
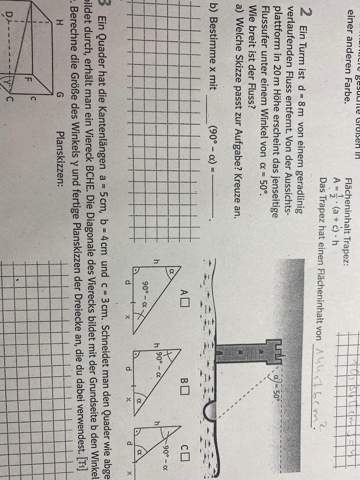
Ich bin für jede erdenkliche Hilfe dankbar!
3 Antworten
Zwischen Turm und horizontaler Linie oben besteht ein rechter Winkel. Alpha ist 50° breit, wie breit ist also der andere Winkel?
Unten hast du auch einen rechten Winkel zwischen Turm und Boden. Wie viel ° hat ein Dreieck? Du kennst den Winkel oben und den rechten Winkel unten, also kennst du auch den dritten Winkel.
Welche Skizze passt also am besten dazu?
---
Nun kennst du die Turmhöhe und den Winkel der dazu passt. Sinus(Winkel1) verhält sich zu Strecke1 wie Sinus(Winkel2) zu Strecke2.
Du weißt nun wie breit das Stück vom Turm bis zum äußeren Flussufer ist (d+x) und die Strecke vom Turm zum inneren Ufer war im Text vorgegeben (d). Daraus lässt sich dann leicht die Breite des Flusses ermitteln (x).
Als Tipp: Die Skizze gibt dir einen falschen Eindruck darüber, wie breit der Fluss ist. Er sieht auf der Skizze sehr viel kleiner aus.
Danke Danke Danke! Ich Dummkopf dachte, der Fluss sei das, was die Wiese ist. Du hast das wirklich verständlich und einfach erklärt und ich werde deine Antwort, wenn möglich, als hilfreichste auszeichnen. Einen schönen Nachmittag/ Abend noch! :)
Ich werde das jetzt mal machen und guck dann mal, ob ich so weiterkomme, aber das war aufjedenfall verständlich und vor allem besser, als trocken die Lösung zu sagen
50 grad da, sind 40 grad dort, die gesuchte strecke ist die gegenkathete, 20m die ankathete
das ist tangens
tangens40=x/20, glaube ich
x ist die gesamtlänge, von turm bis fluss sind 8m
also ist der fluss x-8 breit
Die Skizze B passt zur Aufgabe.
Aufgrund des Sinussatzes gilt:
h/sin(alpha) = (d+x)/sin(90-alpha)
h/sin(alpha) * sin(90-alpha) = d+x
h/sin(alpha) * sin(90-alpha) - d = x
20/sin(50) * sin(40) - 8 = x
x ~ 8.78 m (Flussbreite)
Und wie soll er/sie was lernen, wenn du ihm/ihr das Ergebnis vorgibst?