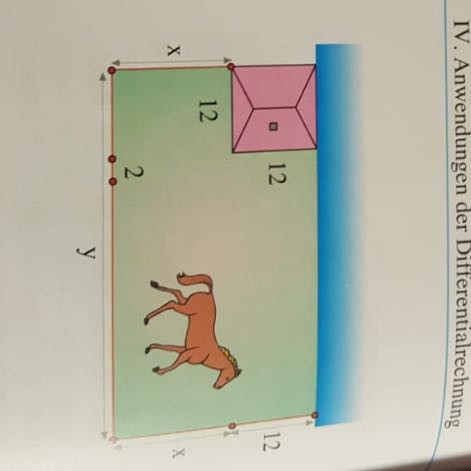
Wie bekomme Ich die maximale Fläche für ein dreiseitigen Zaun?
Ein Farmer will sein Grundstück einzäunen und dies ist direkt am Fluss, so braucht er nur drei Seiten Zu begrenzen. Die Seite mit dem Haus was 12m lang ist braucht 12 m weniger Zaun als die Seite vom Zaun der anderen Seiten des Grundstückes. Außerdem hat die Mittel Zaun Seite ein 2 m Tor was also auch 2 m weniger braucht. Also ist die Linke die einzige von der nichts abgezogen wird.
Wie lang müssen die Zäune sein damit die maximal Fläche entsteht? Hat es was mit Differentialrechnung zu tun?
Ich hoffe jemand kann mir helfen
3 Antworten
Da über dem Bild „Anwendungen der Differentialrechnung“ steht, hat es möglicherweise damit zu tun.
Die Fläche ist demnach …
A = (x + 12) • (y - 2)
Jetzt überlegst Dir, wie Du A möglichst groß bekommst.
ich müsste das einfach nur ausmultizplizieren und dann mithilfe eines Linearem Gleichungssystem es lösen koennen oder?
Korrektur:
Ich seh grad, die Fläche ist …
A = (x + 12) • y
… und die Länge des Zauns …
z = x + y - 2 + x + 12 = 2x + y + 10
Das ist auch nicht die entscheidende Gleichung (aber eine erforderliche), denn Du sollst ja die Fläche maximieren. Dafür mußt Du die Fläche F in Abhängigkeit von x und y darstellen:
F = Y * (x + 12)
Die Fläche des Hauses ziehe ich hier nicht ab, da die grafische Darstellung (Zaun grenzt an die äußere Mauer) ansonsten nicht in Übereinstimmung mit der Aufgabenstellung wäre, wenn man die Hausfläche von der umzäunten Fläche abzöge. In dieser Gleichung kannst Du nun über die andere Gleichung y (oder x) ersetzen und erhieltest eine differenzierbare Gleichung mit einer Variablen. Dann nach Lehrbuch ...
Zaunlänge: 100m = x + (y-2) + (x+12) = 2x + y + 10m
(1) y = 90m - 2x
(2) A = (x + 12m) • y - 144m²
(1) in (2) eingesetzt:
A = x • 90m - 2x² + 1080m² - x • 24m - 144m² = 2x² - x • 66m + 936m²
Ableitung von A gleich Null gesetzt
A' = 0 = 4x - 66m >> x = 16,5m und y = 57m
A = 1480,5m²
Kontrolle: 16,5m + (57m - 2 m) + (16,5m + 12m) = 100m
Wurde ggf. angegeben, wieviel Zaun mittels des verfügbaren Materials gebaut werden könne? So fehlt eine limitierende Größe (und die Angabe der Fläche des Grundstücks machte wenig Sinn) und das Maximum läge bei x,y gegen Unendlich.
Also muss Ich jetzt das lineare Gleichungssystem bilden? Wenn ja wie ?