Was ist der Unterschied zwischen einem t-s und einem t-v Diagramm, weil man die Bewegungen ja unterschiedlich beschreibt?

Eine Bemerkung vorab: Achte beim Posten von Bildern bitte darauf, sie nach Möglichkeit richtig herum einzustellen. Es ist etwas anstrengend, immer den Kopf schief zu halten, und es ist aufwändig, das Bild erst einmal herunterladen zu müssen, um es dann zu drehen.

Die Geschwindigkeit (engl. velocity) ist eigentlich eine Vektorgröße, eine Größe mit Richtung, die üblicherweise mit v⃑, v oder hier mit |v› bezeichnet wird und die man in 3 Komponenten zerlegen kann.

Mit v kann man den Betrag ||v›| bezeichnen, der im Deutschen gewöhnlich auch „Geschwindigkeit“ heißt, während das Englische ein anderes Wort speed dafür nutzt. Ein adäquates deutsches Wort könnte Tempo sein.

Mit v kann aber auch eine der 3 Komponenten, bzw. eine Geschwindigkeit in eine bestimmte Richtung bezeichnen und in diesem Fall auch negativ sein. 

Ist sie während einer Zeitspanne Δt konstant, so sind die räumliche Verschiebung und die Geschwindigkeit einfach aus einander zu errechnen:

(1)    |Δs› = |v›·Δt    ⇔    |v› = |Δs›/Δt.

Im Allgemeinen ist das allerdings nicht der Fall. Die Momentane Geschwindigkeit ist

(2.1)    |v› = |ds›/dt = lim[Δt→0] |Δs›/Δt.

Dies nennt man differenzieren oder ableiten. Der umgekehrte Vorgang nennt sich Integration und ist ein Grenzfall des Aufsummierens von Produkten, hier

(2.2)    |Δs› = ∫_[t₁]^{t₁+Δt} |v›(t)·dt,

wobei man sich |v›(t)·dt = ds für jede Komponente als schmale Streifchen vorstellen kann, aus denen sich die Fläche unter einer Kurve vorstellen kann.

So ein Integral kann auch 0 oder negativ sein. Ist es 0, heißt das nicht, unbedingt dass man sich gar nicht bewegt hat, sondern entweder dies oder dass man zum Ausgangspunkt zurückgekehrt ist.

Eine Wegstrecke Δs oder s während der Zeitspanne Δt errechnet sich als Integral

(3)    Δs = ∫_[t₁]^{t₁+Δt} ||v›|(t)·dt

und enthält keine Richtungsinformation. Auch wenn man zum Ausgangspunkt zurückkehrt, ist das Integral positiv, es sei denn, man hätte sich gar nicht bewegt.

In einem t-s-Diagramm ist v die Steigung/Tangentensteigung von s. Ist s wirklich eine Wegstrecke und v ein Betrag, ist diese Steigung immer positiv. Ist mit s eine bestimmte Richtung und mit v eine Komponente gemeint, kann es auch mal negativ sein.

In einem t-v-Diagramm ist die Beschleunigung die Steigung bzw. Tangentensteigung, und auch die Fläche zwischen der Kurve und der t-Achse hat eine physikalische Bedeutung, nämlich die einer Strecke bzw. Verschiebung.

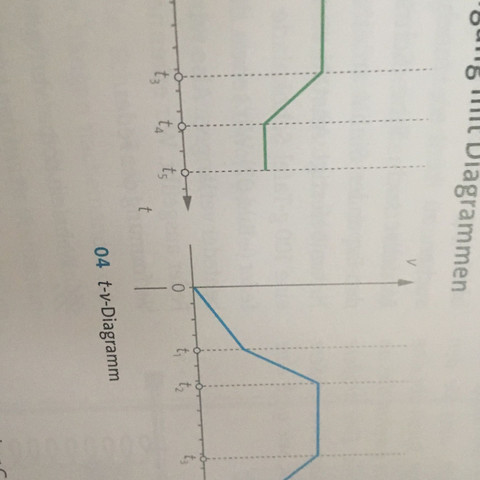
Beim t-s-Diagramm bedeuten die beiden Achsen Zeit (t) und Weg (s); beim t-v-Diagramm sind es Zeit (t) und Geschwindigkeit(v).

s-t beschreibt eine Strecke die in einer bestimmten Zeit bewältigt wird. Die Steigung der Kurver zeigt damit die Geschwindigkeit.

v-t beschreibt die Geschwindigkeit die bei einer bestimmten Zeit vorlag. Die Steigung der Kurver zeigt daher eine Beschleunigung.

Man braucht beide...  Aus dem s-t- Diagramm kann man viel komfortabler die Strecke ablesen.
Bei einem v-t-Diagramm wären hierfür noch nebenrechnungen nötig.

Der Unterschied ist nur...  Naja, beim Einen zeichnet man die strecke auf, beim anderen die geschwindigkeit

t-s = Zeit weg Diagramm
t-v = Zeit Geschwindigkeit Diagramm