Unendliche Reihe, Halbkreis, Mitte?
Hallo.
Ich habe eine Frage zu unendlich Reihen.
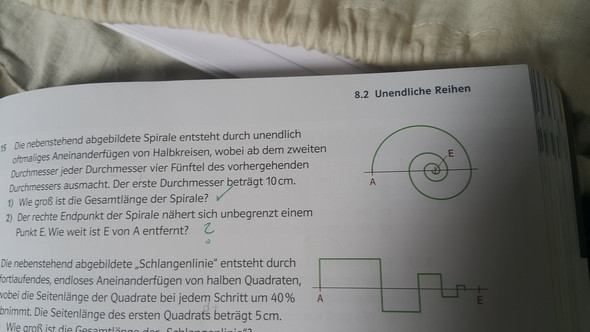
Es sollte dieser Frage ein Bild hinzugefügt sein, auf dem eine Spirale abgebildet ist, die aus unendlich vielen Hakbkreisen besteht. Der erste Durchmesser beträgt dabei 10 cm und jeder Durchmesser macht vier Fünftel des vorhergehenden Durchmessers aus. Ich habe die Länge dieser Spirale als 25 cm ausgerechnet. Stimmt das? Mit der zweiten Frage kann ich aber nichts anfangen. Der Beginn der Spirale wird dabei als Punkt A bezeichnet, das Ende der Spirale als Punkt E. Ich muss die Entfernung A ~> E ermitteln. Wie ist das möglich? Danke!
1 Antwort
25 cm ist nicht richtig, da bist du mit den ersten ~4 Folgengliedern schon drüber.
Der Abstand von A zu E ist 10cm-4/5 * 10cm + (4/5)^2 * 10 cm - ...., also wieder Grenzwert einer unendlichen Reihe.
Edit : Beim zweiten natürlich nicht 10 cm, sondern der Durchmesser eines Kreises, dessen hälfte vom Umfang 10cm ist.
10 ist der Durchmesser, also muss ich mit r*pi > 5*pi rechnen, oder etwa nicht? 5*pi * 1/(4/5) = 25. Oder etwa nicht?
Was aber die zweite Frage betrifft, danke, ich glaube, ich verstehe es schon! :)