Steigung in einem Punkt bestimmen?
Hallo, ich habe eine Frage zu Ana lysis. Die Aufgabe ist, das man von einer Stammfunktion die eingezeichnet ist die normale Funktion einzeichnen soll (also im Prinziep die Ableitung) und dann in einem bestimmten Punkt nährungsweise die Steigung bestimmen soll. Nun stellt sich mir die Frage, woher ich denn weiß wie tief ich die Bögen zeichnen muss (unser Lehrer konnte mir darauf bisher keine wirklich hilfreiche Antwort geben, ich versuche mich immer an dem vorgegeben Graphen zu orientieren) und wie ich eben die Steigung bestimmen soll. Es steht zwar da nährungsweise aber wie weit neben der Antwort darf man denn liegen? Aufgabe 6 auf dem Bild ist gemeint
3 Antworten
die Steigung ermittelst Du ja, indem Du (y2-y1)/(x2-x1) rechnest; je enger x2 und x1 zusammenliegen, desto genauer wird das Ergebnis; ist halt die Frage, wie gut man diese Werte ermitteln kann; messe doch einfach mal die y-Werte bei x=1,75 und 2,25 und rechne die Steigung aus, die Funktion verläuft ja in diesem Bereich "relativ gerade".
wenn Du die 6a) bearbeiten sollst, also g(2), dann ist das die Steigung von G an der Stelle x=2, näherungsweise: (1-1,5)/(2,5-1,5)=-0,5
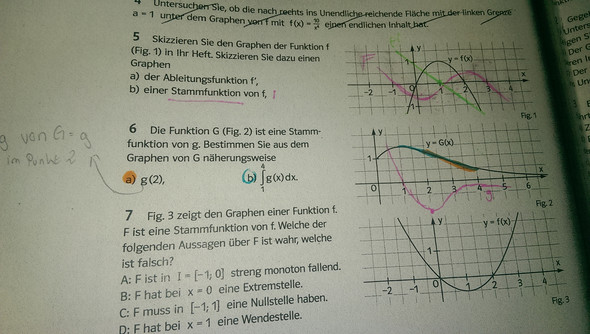
Der Graph der Stammfunktion von g, G, ist ungefähr parabelförmig zwischen x= 0 und x = 2 (sieht zumindest auf dem Bild so aus). Das heißt du könntest also sagen, dass die Funktion G(x) zwischen x=0 und x= 2 eine Parabel sein soll, die nötigen Punkte um die Parabel zu erstellen kannst du ja ablesen. Dann gilt es diese Funktion abzuleiten. Also im Endeffekt in der Form:
G(x) = ax^2 + bx + c für x =[0, 2]
Ableiten:
g(x) = 2ax + b für x =[0, 2]
Dann einfach nur noch 2 in g(x) einsetzen und du solltest näherungsweise die Steigung von G(x) bei x=2 erhalten. (sofern der schwarze Graph nun G(x) ist)
also der schwarze Graph ist G(x) und der pinke die Lösung von unserem Lehrer für g(x)
Und für den pinken Graphen soll ich am Punkt g(2) die Steigung bestimmen. Laut Lehrer ist die Lösung -0,5 aber wie gesagt keine Ahnung wie ich die Ableitung einzeichnen, ich hätte den Graphen ganz anders gezeichnet und wie man dann im Punkt 2 die Steigung bestimmt
Die Ableitung in jedem Punkt zeigt dir die Steigung an...
Dazu müsste ich aber erst mal eine G(x) gegeben haben weil ich sonst nur schätzen kann wo die Ableitung lang läuft und wie ich bereits schrieb fällt es mir besonders bei dem Verlauf von G(x) etwas schwer einzuschätzen wie g(x) verläuft
Das schaut so aus, als sei 2 genau das Minimum an dieser STell, d.h- die Steigung der Kurve kehrt sich in 2 vom negativen ins positive, daher schätze ich dass die STeigung in 2 null ist...
Ich glaube, das ist eine Definition, dass die Ableitung /Steigung in Minima und maxima null ist...
Ich muss ja im selbst gezeichneten Graphen (also dem Pinken der g(x) entspricht) die Steigung im Punkt 2 bestimmen, aber ich hätte nicht mal genau gewusst ob G(x) eine Funktion 3 oder 4 Grades ist und ich hätte glaube ich auch nicht gewusst wie genau der Graph verläuft