Selbstkomplementäre Graphen?

Hey,

herauszufinden ist, ob G selbstkomplementär ist. Soweit ich verstanden habe, muss man also den Komplementärgraphen von G zeichnen (G-Strich) und dann G mit G-Strich vergleichen. Wenn G isomorph zu G-Strich ist, ist G selbstkomplementär, stimmts?

Meine Frage ist, wie finde ich heraus, ob G isomorph zu G-Strich ist.

Danke

Answer 1

[ReimundAcker]

Voraussetzungen:

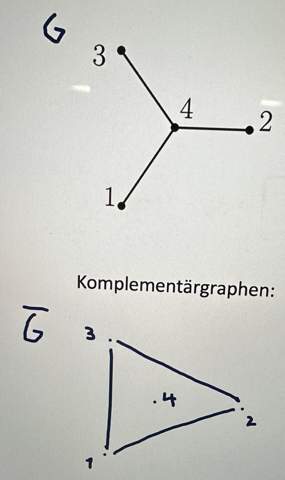
Graph: G = (V, E) mit V = {1, 2, 3, 4} und E = {{1, 4}, {2, 4}, {3, 4}}

Komplementgraph: G' = (V, E') mit E' = {{1, 2}, {1, 3}, {2, 3}}

Behauptung: G ist nicht selbstkomplementär

Indirekter Beweis:

(1)Annahme: G ist selbstkomplementär
(2) ∃ f: V → V [f ist Isomorphismus]     wg. (1)
(3) f ist surjektiv                      wg. (2)
(4) ∃ x∈V [f(x)=4]                       wg. (3) 
(5) ∃ y∈V [{x,y}∈E]                wg. Def. von E 
                                    (jeder Knoten ist verbunden)
(6) {f(x),f(y)}∈E']                   wg. (5) und (2)
(7) {4,f(y)}∈E']                      wg. (4) und (6)
(8) ∃ z∈V [{4,z}∈E']                  wg. (7)
(9) E' = {{1,2}, {1,3}, {2,3}}         wg. Voraussetzung
(10) Widerspruch                       wg. (8) und (9)
(11) G selbstkomplementär⇒Widerspruch  wg. (1) und (10)
(12) G nicht selbstkomplementär        wg. (11)

q.e.d.

Woher ich das weiß: Studium / Ausbildung – LMU München, Dipl. Math., eigene Recherche