Schwere Zahlenfolge weiterführen?
Ich bekomme folgende Zahlenfolge nicht heraus:
8 - 64 - 4 - 64 - 2,8284 - 64 - 2,2974 - 64 - ... - ... -...
Man soll die letzten drei Zahlen angeben. Vermutlich ist es ganz einfach, aber ich komme nicht darauf.
Ich hoffe, jemand kann helfen. Danke im Vorraus!
4 Antworten

Auch wenn Du Dir noch so krumme Zahlenwerte ausdenkst: ohne Randbedingungen (Einschränkungen) gibt es unendlich viele mögliche Algorithmen!
Hier mal 2 auf die schnelle:
a): f(x)= round(pow(64,1/(((x%2)?0:x/2+1)+1))*1e4)/1e4
Das (x%2)?0:x/2+1 {also 0 bei gerade else x/2+1 } kann man auch per cos-Funktion weich bekommen.
pow(x,y) = x^y = x hoch y
b): f(x)= x*(x*(x*(x*(x*(((2777803*x)/3600000-3778347/200000)*x+10437494930/56921699)-10747703/12000)+106299308510/46276649)-54339283930/18782493)+2592071/1875)+8
Per Iterationsrechner der Beweis:
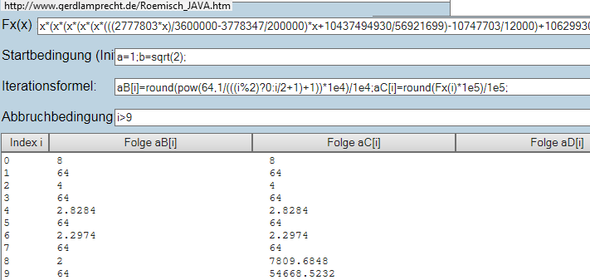
http://www.gerdlamprecht.de/Roemisch_JAVA.htm#x*(x*(x*(x*(x*(((2777803*x)/3600000-3778347/200000)*x+10437494930/56921699)-10747703/12000)+106299308510/46276649)-54339283930/18782493)+2592071/1875)+8@Na=1;b=@Q2);@N@Bi]=round(@P64,1/(((i%252)?0:i/2+1)+1))*1e4)/1e4;@Ci]=round(Fx(i)*1e5)/1e5;@Ni%3E9@N0@N0@N#
(LINK endet mit N# )
siehe Bild
Beide Funktionen könnte ich auf Anfrage noch für Dich plotten (Diagramm) -> dann sieht man die Schnittpunkte genau dort, wo Du Deine Stützstellen angegeben hast.

Mein Ansatz wäre folgender:
- Jede zweite Zahl ist eine 64
- Bei den anderen Zahlen wird jeweils immer die vorherige durch die n-te Wurzel aus 2 dividiert. Das würde in etwa hinkommen (8 / 1-te Wurzel aus 2; 4 / Quadratwurzel aus 2; 2,8284 / 3-te Wurzel aus 2; etc.), allerdings würde 2,2974 dann nicht ganz passen.
Daher könnte die Lösung wie folgt aussehen:
8 - 64 - 4 - 64 - 2,8284 - 64 - 2,2974 - 64 - 1,8877 - 64 - 1,6434

Erstmal: man kann eine Zahlenfolge immer auf unterschiedliche Wege fortführen, nur weil man ein Muster zu erkennen meint heißt das nicht, dass dies auch das "richtige" Muster ist.
Hier ist das Muster, das man wohl erkennen soll, dass man abwechselnd potenziert und Wurzeln zieht.
Dagegen spricht, dass 2.8284 nicht die 4. Wurzel von 64, also die Wurzel von 8, ist. Sondern nur eine gerundete Annäherung.
Analog bei 2.2974.
Wenn in der Aufgabenstellung also nichts von gerundeten Werten erwähnt wird kann man sich lange auf die Suche nach einem anderen Muster machen.
Nach meiner Idee und unter der Voraussetzung, dass wir die Ungenauigkeit der Zahlenwerte vernachlässigen, wäre die Fortsetzung ... - 2 - 64 - 64^(1/7)

naja, der Versuch "die ganze Zahl" aufzuschreiben wäre wahrscheinlich auch ein Fehler gewesen, zumindest wenn du sie als Dezimalzahl hättest darstellen wollen.

Pass auf du ziehst von 64 die wurzel und dann hast du 8. Dann ziehst du von 64 die dritte wurzel und bekommst 4 denn 4*4*4 ist 64. Dann ziehst du die vierte wurzel und bekommst 2,82...usw dann folgt so die 5. 6. 7. Wurzel..
Dankeschön. :) Ich habe sie selbst gerundet, wollte nicht die ganze Zahl aufschreiben. Wusste nicht, dass das ein Fehler war:D