Satz des Pythagoras, Sachaufgabe?
Hallo, ich komme bei folgender Sachaufgabe nicht weiter:
Person A und Person B haben für eine Gartenparty zwischen zwei Bäumen in 3m Höhe ein 4,60m langes Seil gespannt und in seiner Mitte eine Partysonne (Durchmesser 80cm) aufgehängt. Die Bäume stehen 4,50m auseinander. Wie groß darf ein Gast höchstens sein, damit er sich ohne zu bücken unter der Partysonne durchgehen kann.
Wie soll ich hier den Satz des Pythagoras anwenden?
Bitte um Hilfe mit Rechnung und Ergebnis.
Danke!
LG
3 Antworten
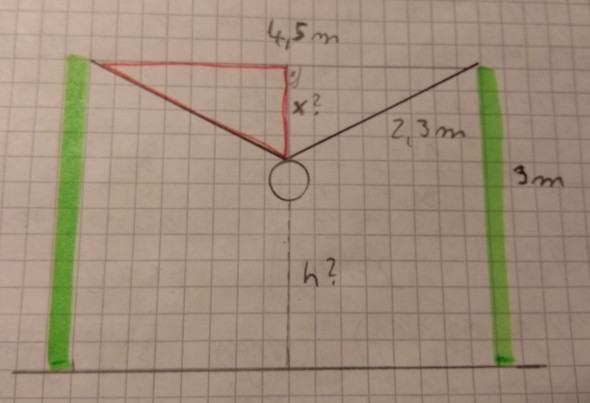
Eine recht grobe, nicht maßstabsgetreue Skizze, wie ich die Aufgabe sehe:

H ist gesucht.
h = 3 m - "Durchhang" des Seils - Durchmesser Partysonne
Den Durchhang des Seils habe ich mal X genannt.
Wie berechnet man x?
Dafür habe ich mit rot mal ein rechtwinkliges Dreieck als Hilfe für den Pythagoras eingezeichnet.
Ich habs verstanden! Danke! Somit darf die Person max. 1,72m groß sein. LG
Du hattest - im Gegensatz zu mir - wohl Dein Lineal nicht verlegt. 😉
eigentlich ist das durchhängende Seil eine Kettenlinie
https://de.wikipedia.org/wiki/Kettenlinie_%28Mathematik%29
aber das ist wohl zu heavy für dieses Problem
............
ich kann mir hier nur vorstellen , daß die "Länge des Durchhängens (LdD) " in der Mitte mit dem SdP bestimmen soll, wobei man das Seil sich als eine gerade Strecke denkt.
Dann wäre (4.60/2)² = (LdD)² + (4.50/2)²
und LdD ca 47 cm
Also wird die Paatysonne 47 + Durchmesser tief hängen
PS : Es ist ja doch keine Kettenlinie , denn es ist eine "Last" dran , die das Seil spannt. :)) Also denke ich , so gehts , wie ich schrieb.
Ich habs verstanden! Danke! Somit darf die Person max. 1,72m groß sein. LG
Du hast ein gleichschenkliges Dreieck, dessen lange Seite 4,50 m ist und die beiden anderen sind zusammen 4,60. Du musst die Höhe berechnen, dann weist Du wie viel das Seil in der Mitte durchhängt.
Dazu den Durchmesser der Partysonne addieren und von den 3 m abziehen.
Ich habe eine Zeichnung "hingeschmiert", aus der Du vielleicht klug wirst?


P.S.: Das Ganze ist übrigens rein mathematisch zu sehen. Ein Ingenieur würde wohl "mit den Ohren schlackern", weil viele Voraussetzungen, die nötig sind, nicht ausdrücklich gegeben wurden.
Z.B. kann man natürlich ein 4,60 m langes Seil nicht ohne Verluste zwischen zwei Bäume spanne. Und weder Bäume noch Untergrund sind in der Natur ideal gerade und rechtwinklig.
Ich habs verstanden! Danke! Somit darf die Person max. 1,72m groß sein. LG