Nullstelle(n) von Funktion f(x) =x^2 +e?
Woran kann man bei der Funktion f(x) =x^2+e erkennen, ob sie Nullstellen hat?
LG
7 Antworten
Mit der Tatsache, dass e die Eulerzahl ist, hat es natürlich überhaupt nichts zu tun. Jeder Summand a > 0 würde die Parabel nach oben schieben, so dass sie keine reelle Nullstellen mehr hätte.
Und ebensowenig geheimniswoll ist, dass f(x) = x² - e zwei Nullstellen hat, x² - 2 aber auch.
Bei Aufgaben wie diese kannst du dir die Funktion auch ganz einfach am Pc mit einem Programm kostenlos zeichnen lassen, z.B. GeoGebra. Vielleicht fällt es dir auch in Zukunft dann leichter ;)
Stimmt ;) du musst einfach logisch denken.
Wenn die Parabel nach unte geöffnet ist (-a) dann kommt es drauf an ob der Scheitelpunkt positiv ist (+1/+5) (2. nullstellen) oder negativ (-1/3)(keine nullstelle) .beispiel siehe Foto
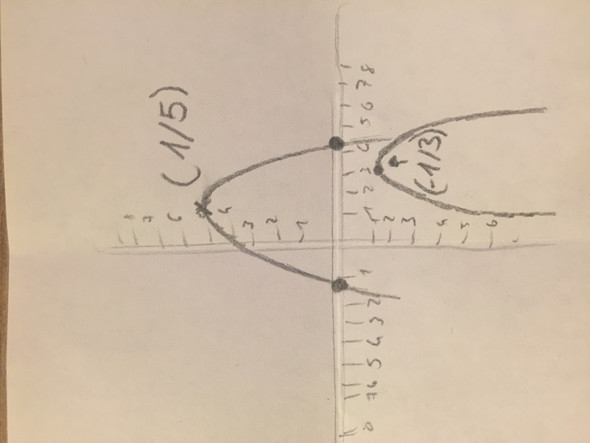
Für f(x) = ax²+c und c>0 hat f keine reellen Nullstellen.
Hinweis : e ist die eulerische Zahl 2,7....
Die Funktion wurde um die Zahl e nach oben in Y Richtung verschoben.
Hat keine Nullstelle. Die Zahl e (2,71..) beschreibt die Verschiebung der Funktion auf der y-Achse. Das bedeutet dass die Funktion die x-Achse nicht schneidet, also nicht berührt.