Natürliche Exponentialfunktion und Tangente?
Hallo, ich komme bei nr. 3 auf dem Arbeitsblatt nicht weiter. Wenn jemand mir helfen könnte, wäre das sehr nett.
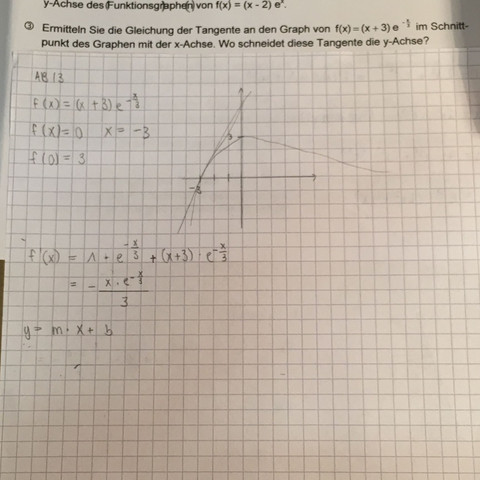
2 Antworten
Das Ergebnis Deiner Ableitung ist richtig; Dein erster Schritt dahin jedoch nicht...!?! (Wohl 'nen Ableitungsrechner "befragt" :) )
f'(x)=1 * e^(-x/3) + (x+3) * e^(-x/3) * (-1/3) [=innere Ableitung von e !]
Jetzt alles auf den Hauptnenner 3 bringen und zusammenfassen:
=(3e^(-x/3) -xe^(-x/3) - 3e^(-x/3)) / 3 = -xe^(-x/3)/3
Jetzt f'(-3) ausrechnen, und Du hast das m der Tangente. Dann noch diese Nullstelle einsetzen und b ausrechnen...
siehe Mathe-Formelbuch "Differentialgeometrie"
Tangentengleichung yt=ft(x)=f´(xo)*(x-xo)+f(xo)
Normalengleichung yn=fn(x)=-1/f´(xo)*(x-xo)+f(xo)
xo ist die Stelle,wo die Tangente liegen soll
f(x)=(x+3)*e^(-1/3*x) Nullstelle bei 0=x+3 also bei x=xo=-3
f(xo)=f(-3)=(-3+3)*e^(-1/3*-3)=0*e^1=0
nun ableiten mit der Produktregel (u*v)´=u´*v+u*v´
u=x+3 abgeleitet u´=1
v=e^(-1/3*x) abgeleitet v´=-1/3*e^(-1/3*x) eingesetzt
f´(x)=1*e^(-1/3*x)+(x+3)*(-1/3)*e^(-1/3*x)=e^(-1/3*x)*(1+(x+3)*-1/3)
f´(x)=e^(-1/3*x)*(1-1/3*x-1)
f´(x)=e^(-1/3*x)*(-1/3)*x mit x=xo=-3
f´(-3)=e^1*(-1/3*-3)=e^1
eingesetzt
yt=ft(x)=f´(xo)*(x-(-3)+0=e^1*x+3*e^1
Tangentengleichung also yt=ft(x)=e^1*x+3*e^1
Schnittpunkt mit der y-Achse bei x=0 ergibt
ft(0)=e^1*0+3*e^1=8,1348
Prüfe auf Rechen-u. Tippfehler
Danke für die Antwort! Wie kommt man bei der tangentengleichung auf das +3e^1 ?