Näherungsweise die Ableitung bestimmen?
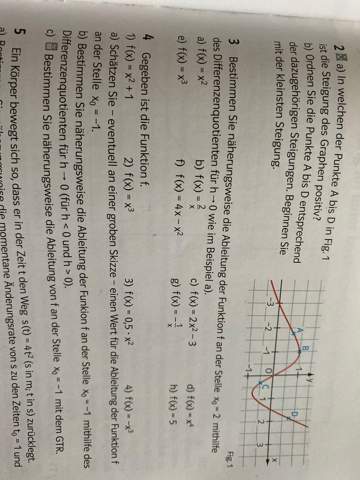
das wäre die Aufgabe 3. Kann mir das jemand erklären. Zum Beispiel bei d) und f) .
4 Antworten

Der Differenzenquotient ist gegeben als die Steigung der Sekante durch zwei Punkte P1 und P2 einer Funktion f(x):
(y2 - y1) / (x2 - x1) (1)
x2 = x1 + h <=> h = x2 - x1
(y2 - y1) / h (2)
bzw.
[f(x1+h) - f(x1)] / h (3)
Setz in (3) deine Funktion ein.
d) f(x) = x^4
[(x + h)^4 - x^4] / h (4)
Damit der Nenner für h --> 0 nicht null wird, musst du im Nenner h als Faktor irgendwie wegkriegen. Dazu musst du den Bruch so umformen, dass du h herauskürzen kannst. Hier genügt es, lediglich den Zähler auszurechnen und zu vereinfachen, bis im Zähler h als Faktor vorliegt.
(x + h)^4 = (x^2 + 2hx + h^2)(x^2 + 2hx + h^2) = x^4 + 4 hx^3 + 6 h^2*x^2 + 4 h^3*x + h^4,
(x + h)^4 - x^4 = 4 hx^3 + 6 h^2 * x^2 + 4 h^3 * x = 2 hx (2 x^2 + 3 hx + 2 h^2)
Sodann kannst du den Bruch mit h kürzen und du erhältst:
[(x + h)^4 - x^4] / h = 2x (2 x^2 + 3hx + 2 h^2)
Jetzt bildest du den Differentialquotient (limes aus dem Differenzenquotient für h --> 0).
f'(x) = lim {h --> 0} 2x (2 x^2 + 3hx + 2 h^2)
Wie du siehst, werden die letzten zwei Summanden null für h --> 0. Mittels Grenzwertbildung erntest du demnach
f'(x) = 4x^3
f'(x) liefert die Tangentensteigung für jedes beliebige x ∈ D der Funktion f(x) und ist somit ihre Steigungsfunktion (als ihre erste Ableitung genannt).
Setz x = 2 in die erste Ableitung ein und du bekommst die Lösung für d).

3f)
Differenzenquotient für x0=2:
Grenzwert für h --> 0 ist 0
die Ableitung an der Stelle x=2 ist null

Du setzt die stelle ein un berechnet dann für kleiner werdende h den wert und Butz diese dann für die Abschätzung

In Formel für Differenzenquotienten einsetzen. Das Ausrechnen artet dann wegen der Exponenten bei ^4 in Arbeit aus... Danach kann man h kürzen.