Mathe Aufgabe - Metallkugel im Zylinder
Hallo!
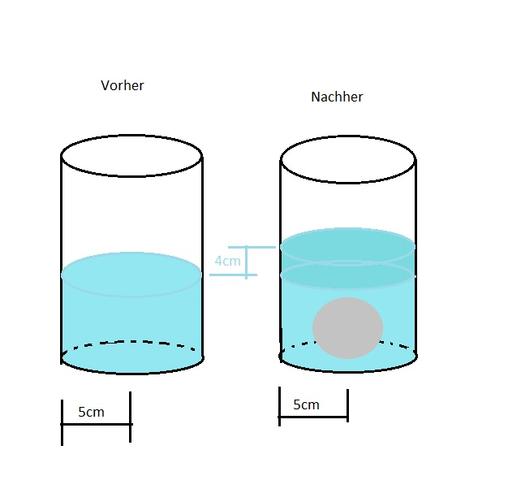
Die Aufgabe lautet: Ein Messbecher in Zylinderform ist zum Teil mit Wasser gefüllt. Der Zylinder hat einen Radius von 5 cm. In den Zylinder wird eine Metallkugel geworfen. Dadurch steigt der Wasserspiegel um 4 cm.
Kann mir jemand bei der Aufgabe helfen?
3 Antworten

Das Volumen, das dann im Zylinder dazu gekommen ist ist ja das von der Kugel verdrängte Wasser. Ich habe es in meine Zeichnung dunkler eingefärbt. Der Wasserspiegel ist um 4 cm gestiegen. Also ist
4cm * pi 25cm²=V(Kugel)=100cm³ pi
Formel für Kugelvolumen: V=4/3 pi r³
100cm³ pi=4/3 pi r³
75=r³ r=4,21...cm


gut zu wissen... ich nutze immer Umschalt-Enter (aber das ist auch für neuen Absatz).

die Kugel hat ein volumen wie ein Zylinder mit dem Radius 5cm und der Höhe 4cm. Also pi mal 4² * 5 und das Volumen in die volumenformel für die Kugel einsetzen die lautet V = 4/3 * pi * r³, und nach r auflösen zum schluss mit der dritten wurzel und dann hast du es.

Vzyl = r² * pi * h = 5² * pi * 4 = 100 pi
Vkug =100 pi = 4/3 * r³ * pi
=> 100 = 4/3 * r³
=> r = ca. 4,22 cm
Der Radius der Kugel beträgt ca. 4,22 cm

Nunja. Das Problem ist ja, dass die höhe nicht 4 sein kann, da, die Höhe erst durch das ...öhm "Einführen" der Kügel um 4 cm stieg.

Wenn genug Wasser im Zylinder ist, sodass die Kugel vollkommen vom Wasser bedeckt ist, dann ist meine Berechnung richtig - überleg mal, es ja hier nur darum, um wie viel die Wasserhöhe steigt, nicht welche endgültige Höhe sie erreicht

Das dann gleich mit einer Zeichung zu belegen, ganz schön toll.
Ich kriege es immer nur verbal hin.