Mathe 2 Tangenten in einem Punkt
Hallo
Ich häng mal wieder an einer Matheaufgabe fest und bin mir nicht sicher. Folgende Aufgabenstellung: d) Florian behauptet: "Durch jeden Punkt des Graphen f gibt es 2 Geraden, die Tangenten an diesem Graphen sind." Erörtern sie diese Behauptung ohne Rechnung ausführlich anhand von Skizzen. Präzisieren sie ggf. Florians Behauptung, begründen Sie ihre Antwort und belegen Sie Ihre Ergebnisse in Spezialfällen rechnerisch!
Also ich bin der Meinung, dass es in jedem Punkt nur eine Tangente geben kann, da jeder Punkt nur eine momentane Änderungsrate hat und die Ableitungsfunktion jedem Punkt des Graphen nur einen Wert als Steigung zuordnet. Ist das richtig oder gibt es da Sonderfälle? Und wie soll ich das mit einer Skizze begründen?
e) Überprüfen Sie Ihre Erkenntnisse aus Teilaufgabe d) an den Funktionen g(x) = x^3+0,5x und h(x)=(x+2)x(4-x)
Wie soll ich es da begründen?
5 Antworten
d) Florian behauptet: "Durch jeden Punkt des Graphen f gibt es 2 Geraden, die Tangenten an diesem Graphen sind."
Hier müsste eigentlich stehen, welche Funktion f gemeint ist, oder zumindest, welche Art von Funktion.
Aber wahrscheinlich habt ihr ein Oberthema, wahrscheinlich sind es ganzrationale Funktionen (die Beispiele in e) deuten darauf hin). Also sowas wie f(x)=Polynom
Erörtern sie diese Behauptung ohne Rechnung ausführlich anhand von Skizzen. Präzisieren sie ggf. Florians Behauptung, begründen Sie ihre Antwort und belegen Sie Ihre Erg
Mach dir eine Skizze ihgendeines Funktionsgraphen, also nimm irgend eine Kurve, die Graph einer Funktion sein könnte. Du kannst dann sagen, dass du mit dem Lineal immer an jedem Punkt eine Tangete zeichen kannst, nie zwei.
Präzisieren sie ggf. Florians Behauptung,
Es würde eigentlich heißen, dass die Ableitung keine Funktion wäre, denn sie hätte dann für ein x zwei Werte, was für eine Funktion nicht sein kann. Noch anders ausgedrückt: Es würde heißen, dass es da gar keine Ableitungsfunktion gäbe.
begründen Sie ihre Antwort
Aber du kennst ja die Ableitungsregeln und kannst die verwenden. Das Ergebnis ist immer eine Funktion.
und belegen Sie Ihre Ergebnisse in Spezialfällen rechnerisch!
Nimm halt ein paar Beispiele.
Also ich bin der Meinung, dass es in jedem Punkt nur eine Tangente geben kann, ...
Ja. Für solche Funktionen, wie ihr sie (vermutlich) betrachtet, ist das richtig.
Ist das richtig oder gibt es da Sonderfälle?
Gibt es. Einfachstes Beispiel ist die Betragsfunktion:
f(x) = |x|
Die hat bei x=0 keine eindeutig bestimmte Tangente (zeichne mal den Graph). Rechnerisch käme man da sowohl auf die Steigung -1 als auch auf die Steigung 1. Die Ableitung dieser Funktion ist bei x=0 nicht definiert.
Aber die Betragsfunktion kann ja auch nicht als Polynom geschrieben werden, sie gehört zu den stückweise stetigen Funktionen. Und die sind (vermutlich) bei euch nicht das Thema.
Und wie soll ich das mit einer Skizze begründen?
Steht schon oben. Einfach anschaulich, man sieht es, dass da nur eine Tangente möglich ist.
e) Überprüfen Sie Ihre Erkenntnisse aus Teilaufgabe d) an den Funktionen g(x) = x^3+0,5x und h(x)=(x+2)x(4-x)
Du verwendest die Ableitungsregeln, die Ableitungen sind wieder Funktionen, die Ableitung gibt die Steigung der Tangete in einem Punkt -- und da eine Funtion an jeder Stelle nur einen Wert hat, gibts an jeder Stelle auch nur eine Tangente
Bei kubischen Funktionen kann ich das verstehen, da jeder Punkte eine eigene Tangente hat und gleichzeitig von einer Tangente eines anderen Punkts des Graphen geschnitten wird. Bei rein konvexen Funktionen hast du allerdings ein Problem, denn da kann ich mir beim besten Willen nicht erklären, wie zwei Tangenten in einem Punkt des Grafen zusammenkommen.
Hi,
die Aufgabenstellung ist ein wenig irreführend.
Durch jeden Punkt des Graphen f gibt es 2 Geraden, die Tangenten an diesem Graphen sind.
Man muss aufpassen: Florian behauptet nicht, dass diese beiden Geraden auch Tangenten an diesem Punkt sein müssen, sondern nur Tangenten an diesem Graphen. D.h. sie können den Graphen in dem Punkt selbst ruhig schneiden, Hauptsache sie berührt ihn in irgendeinem anderen Punkt. Ich will dir das Problem in einer Skizze verdeutlichen.
Ich habe unten einen Punkt markiert, an dem ich die Behauptung zeigen möchte. Ich habe die Tangenten t1 und t2 an den Graphen eingezeichnet. Beide gehen durch den Punkt und beide sind in der Tat Tangenten an den Graphen, nur ist eine davon eben keine Tangente an diesem Punkt.
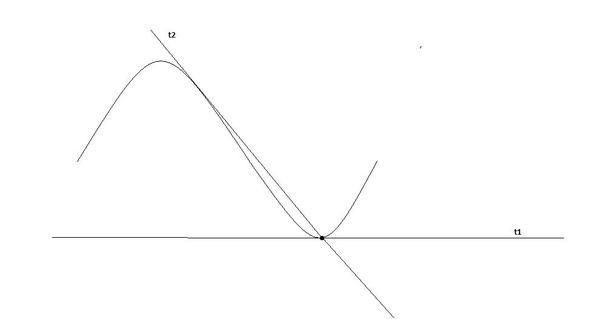
Man muss aufpassen: Florian behauptet nicht, dass diese beiden Geraden auch Tangenten an diesem Punkt sein müssen, sondern nur Tangenten an diesem Graphen.
Ahh, du hast recht, da hatte ich zu flüchtig gelesen.
wie ist es, wenn f eine lineare Funktion beschreibt;
Aufgabenstellung: 2 Geraden ; oder 2 verschiedene Geraden?
Das ist eine schlechte Aufgabenstellung. Wenn ich es korrekt verstanden habe, hast du schon recht. Lass es einfach sein und fordere morgen deine Lehrerin auf, anständige Aufgabestellungen zu geben, falls sie Stress machen sollte.
Ja, diese Aufgabenstellung hat mich auch schon verwundert. Aber Sie steht in einem neuem Mathebuch drin, welches für das Abi 2013/14 ist o.O Ich werde es ihr morgen sagen ;-)