Kann mir jemand bei Mathematik zum Thema Vektoren helfen?
Ich muss Aufgabe 15 machen, verstehe das aber nicht. Kann mir bitte jemand helfen?
3 Antworten
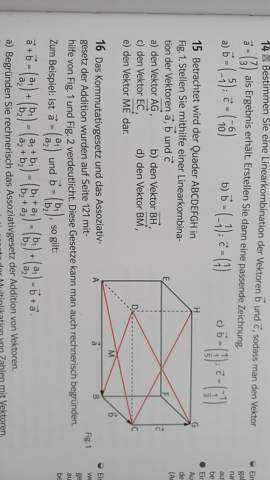
Jeder der Vektoren tritt ja viermal auf. Z.B. ist der Vektor a auch EF, DC und HG.
Wenn man z.B. den Vektor BH sucht, läuft man die Kanten des Quaders von B nach H ab und addiert (vorzeichenrichtig) die Vektoren, also b + c - a. (-a deshalb, weil wir von G nach H laufen, der Vektor a aber von H nach G gerichtet ist.
ME ist etwas schwieriger, man läuft von M um -b/2 zur Kante AB, dann um -a/2 nach A und dann um c nach E, das ist -a/2 -b/2 + c.
Das ist nichts weiter,als eine Vektoraddition und/oder Vektorsuntraktion
1) Großbuchstaben verwendet man für Punkte in einem x-y-z-Koordinatensystem
2) Kleinbuchstaben (mit einem kleinen Pfeil darüber ) als Vektoren
A(ax/ay/az) → Ortsvektor a(ax/ay/az)
B(bx/by/bz) → Ortsvektor b(bx/by/bz)
Richtungsvektor m von Punkt A nach Punkt B → b=a+m → AB=m=b-a
als Richtungsvektor haben wir in der Zeichnung gegeben
Von Punkt A nach Punkt B → a
Von Punkt B nach Punkt C → b
Von Punkt C nach Punkt G → c
a) Richtungsvektor von Punkt A nach Punkt G → AG=m=a+b+c (ist die Vektoraddition)
Bdeutet:Von Punkt A nach B mit Richtungsvektor a
Von Punkt B nach Punkt C mit Richtungsvektor b
Von Punkt A nach Punkt C wäre dann AC=m=a+b
Von Punkt C nach Punkt G mit Richtungsvektor c
also AG=m=a+b+c
b) BH=m=b+c-a von B nach C und von da nach Punkt H
Hinweis: -1*a kehrt den Richtungsvektor um → Pfeil zeigt dann in entgegengesetzter Richtung
c) EC=m=a+b-c
d) BM=m=1/2*BD=1/2*(b-a) → Richtungsvektor BD=m=b-a
Infos,vergrößern und/oder herunterladen
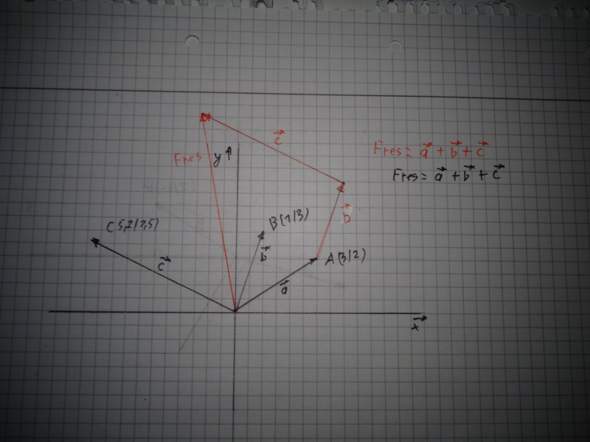
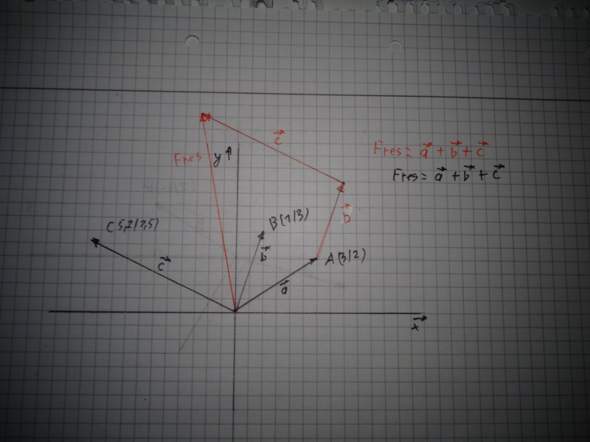
Überlege einfach, mit Hilfe welcher Vektoren du vom Punkt a zum Punkt G kommst. Da wirst du feststellen, das
AG=a+b+c ist. (Die Vektorenpfeile fehlen hier natürlich)
Mach das mit den anderen Strecken genauso.