Kann jemand mir bei der quadratischen Ergänzung dieser Gleichung helfen:)?

 0,5x (x+24) = 56

Answer 1

[Volens]

Quadratische Ergänzung

Da alle Gleichungen unabhängig vom Faktor vor x²
dieselben Lösungen haben wie die passende 
Normalparabel, erstelle ich diese zunächst.

0,5x (x+24)         =  56  | *2
   x (x + 24)       = 112  | ausklammern
   x² + 24x         = 112  | quadrat. ergänzen
                             Dafür muss 24 halbiert
                             und quadriert werden
                             und dann subtrahiert.
x² + 24x + 12² -144 = 112  | +144
x² + 24x + 12²      = 256  | Binom herstellen
  (x + 12)²         = 256      | √
      x + 12        = ±16      | -12
      x₁₂            = -12 ± 16 
      x₁             =    4
      x₂             =  -28

Woher ich das weiß: eigene Erfahrung – Unterricht - ohne Schulbetrieb

Answer 2

[Willy1729]

Hallo,

multipliziere die Gleichung mit 2:

x*(x+24)=112

Ausmultiplizieren der Klammer:

x²+24x=112

x²+24x-112=0

Da -112=28*(-4) und 28-4=24, kannst Du die Gleichung zu
(x+28)*(x-4)=0 umwandeln und so die Nullstellen x1=-28 und x2=4 direkt ablesen.

Herzliche Grüße,

Willy

Comments

[Tannibi]

Aber es sollte doch quadratische Ergänzung sein.

[Willy1729]

@Tannibi

Hab ich überlesen.

Dann: 0,5*(x²+24x)=56

Quadratische Ergänzung ist das Quadrat der Hälfte von 24, also 144:

0,5(x²+24x+144)-0,5*144=56
0,5*(x+12)²-72=56

0,5*(x+12)²=128

(x+12)²=256

x+12=±16

x1=16-12=4
x2=-16-12=-28

Answer 3

[LORDderANALYSE]

Damit wir die quadratische Ergänzung anwenden können müssen wir hier zuerst diese Gleichung in eine quaddratische Funktion umwandeln:

$\frac{1}{2}\cdot x\cdot\left(x+24\right)=56\mid\cdot2$

$x\cdot\left(x+24\right)=112$

ausmultiplizieren der Klammer:

$x\cdot x+24\cdot x=112$

$x^2+24x=112\mid-112$

$x^2+24x-112=0$

Wir wissen das für eine quadratische Funktion der Form gilt:

$ax^2+bx^1+cx^0=0$

(x^0=1, also kann es wegeelassen werden)

Und die Quadratische Ergänzung:

$+\left(x+12\right)^2$

(also +12^2 bzw. 144)

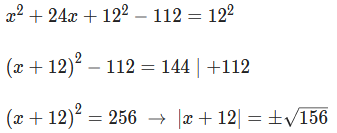
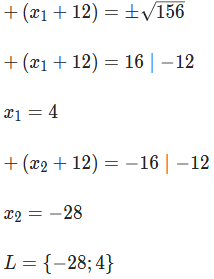
Ich hoffe, dass das Ihnen weiter hilft.^^

Bei Fragen Diesbezüglich stehe ich Ihnen natürlich zur Verfügung. ;)

Woher ich das weiß: Studium / Ausbildung – Mathematikstudium

Comments

[LORDderANALYSE]

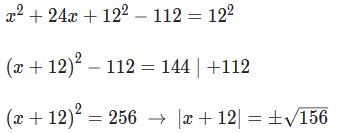
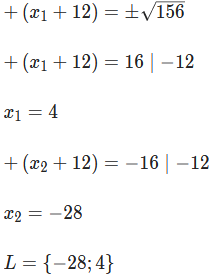
Wenn man sich fragt wieso ich -112 gerechnet habe...

Ich habe keine Ahnung...

Vielleicht langeweile.

[Volens]

@LORDderANALYSE

Wie man auf 112 kommt und dann weiterrechnet, steht in meiner Antwort.

[LORDderANALYSE]

@Volens

Ich meinte damit, dass ich die 112 von der rechten Seite weggerechnet habe nur um sie dnn wieder hinzurechnen, obwohl es vollkomen unnötig war und mir sogar noch mehr Mühen bereitet hat.^^

[Volens]

@LORDderANALYSE

Bei dieser Aufgabenstellung war es eigentlich ökonomischer, die Konstante rechts stehen zu lassen und nachher mit dem b² der Quadratischen Ergänzung zu verrechnen.

Answer 4

[schaafus]

0,5x^2+12x=56

0,5(x^2+24x +144)=128

(x+12)^2=256

Comments

[Willy1729]

Den Scheitelpunkt einer Gleichung bestimmen zu wollen ist schon etwas gewagt.