Kann es jemand erklären?

Ich räume gerade auf und finde mein Arbeitshäft aus 6 Klasse in einen Regal und ich gucke mir die nr.3 an und checke nichts wie früher!

Ich erwartete das wenn ich älter werde das ich schlauer werde 🤓☝️!

Nö wurde ich nicht:(

Answer 1

[mihisu]

Zunächst einmal kann man zwei Brüche mit gleichem Nenner addieren/subtrahieren, indem man die Zähler (also die oberen Teile der Brüche) addiert/subtrahiert und den gemeinsamen Nenner als Nenner beibehält.

Beispiel:

$\frac{9}{14}+\frac{11}{14}=\frac{9+11}{14}=\frac{20}{14}$

Nun soll man das Ergebnis noch (wenn möglich) kürzen und als gemischten Bruch schreiben.

20 und 14 sind beide durch 2 teilbar, da 20 = 2 ⋅ 10 und 14 = 2 ⋅ 7 ist. Dementsprechend kann man den Bruch 20/14 mit 2 kürzen. [Schau also, durch welche Zahlen Zähler und Nenner des Bruches teilbar sind, und ob es da gemeinsame Teiler gibt, mit denen man dann den Bruch kürzen kann.]

$\frac{20}{14}=\frac{2\cdot 10}{2\cdot 7}=\frac{10}{7}$

Wenn nun der Zähler (oberer Teil des Bruches) größer als der Nenner (unterer Teil) des Bruches ist, so kann man schauen, wie oft der Nenner in den Zähler passt.

Beim Beispiel mit 10/7 passt 7 nun 1-mal in 10 rein. [Denn 1-mal 7 ist 7, was kleiner oder gleich 10 ist. Und 2-mal 7 wäre 14, was bereits größer als 10 wäre.]

Damit hat man den ganzzahligen Anteil (hier: 1) gefunden. Für den restlichen Bruchteil zieht man nun beim Zähler das entsprechende Vielfache des Nenners ab. Im konkreten Beispiel ist dann 10 - 1 ⋅ 7 = 10 - 7 = 3, weshalb noch 3/10 als restlicher Bruchteil verbleibt. Demnach kann man 10/7 auch als 1 + 3/7 schreiben und erhält dann dementsprechend die gesuchte Schreibweise 1 3/7 als gemischten Bruch. [Bei der Schreibweise als gemischter Bruch wird das Pluszeichen zwischen der ganzen Zahl und dem restlichen Bruchteil weggelassen.]

$\frac{10}{7}=\frac{1\cdot 7+3}{7}=1+\frac{3}{7}=1\frac{3}{7}$

====== a) ======

$\frac{9}{14}+\frac{11}{14}=\frac{9+11}{14}=\frac{20}{14}=\frac{2\cdot 10}{2\cdot 7}=\frac{10}{7}=\frac{1\cdot 7+3}{7}=1+\frac{3}{7}=1\frac{3}{7}$

[Das muss man nicht unbedingt so ausführlich aufschreiben. Da kann man auch Zwischenschritte weglassen, die klar erscheinen.]

$\frac{19}{20}+\frac{17}{20}=\frac{19+17}{20}=\frac{36}{20}=\frac{4\cdot 9}{4\cdot 5}=\frac{9}{5}=\frac{1\cdot 5+4}{5}=1+\frac{4}{5}=1\frac{4}{5}$

====== b) ======

$\frac{13}{18}+\frac{7}{18}=\frac{13+7}{18}=\frac{20}{18}=\frac{2\cdot 10}{2\cdot 9}=\frac{10}{9}=\frac{1\cdot 9+1}{9}=1+\frac{1}{9}=1\frac{1}{9}$

$\frac{14}{15}+\frac{8}{15}=\frac{14+8}{15}=\frac{22}{15}=\frac{1\cdot 15+7}{15}=1+\frac{7}{15}=1\frac{7}{15}$

====== c) ======

$\frac{17}{24}+\frac{19}{24}=\frac{17+19}{24}=\frac{36}{24}=\frac{12\cdot 3}{12\cdot 2}=\frac{3}{2}=\frac{1\cdot 2+1}{2}=1+\frac{1}{2}=1\frac{1}{2}$

$\frac{11}{16}+\frac{7}{16}=\frac{11+7}{16}=\frac{18}{16}=\frac{2\cdot 9}{2\cdot 8}=\frac{9}{8}=\frac{1\cdot 8+1}{8}=1+\frac{1}{8}=1\frac{1}{8}$

====== Ergänzung ======

Hier noch eine grafische Veranschaulichung zur ersten Rechenaufgabe...

Answer 2

[FuerFortnite666]

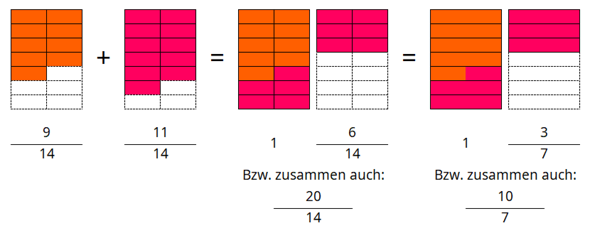
Du addierst kürzt und machst aus 6/5 1 und 1/5

Answer 3

[Juli123988235]

Ist einfach musst die Obern Zahlen addieren und fertig

Comments

[JensR77]

Und noch kürzen, erst dann ist man laut Arbeitsanweisung fertig.

Answer 4

[Rubezahl2000]

So geht's:

$\frac{9}{14}\ +\ \frac{11}{14}\ =\ \frac{20}{14}\ =\ 1\ \frac{6}{14}\ =\ 1\ \frac{3}{7}$

Comments

[Makoo433]

Danke sehr später verdienst du stern