Ist die zweite Ableitung der Punkt, wo eine Funktion am stärksten steigt/fällt?
Eigentlich schon, oder? Da bei der zweiten Ableitung einer Funktion ja der Wendepunkt ist.
4 Antworten
Du hast nicht Unrecht , aber es gilt nicht immer und nicht so wie du es schreibst.
.
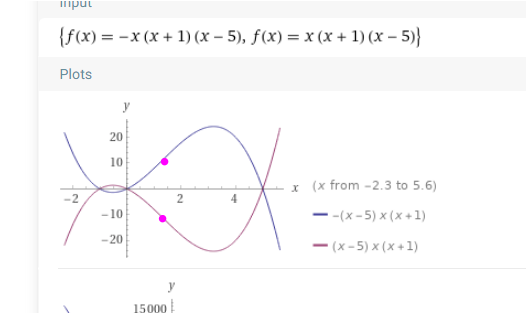
f(x) = minus x(x+1)(x-5)
und
f(x) = plus x(x+1)(x-5)
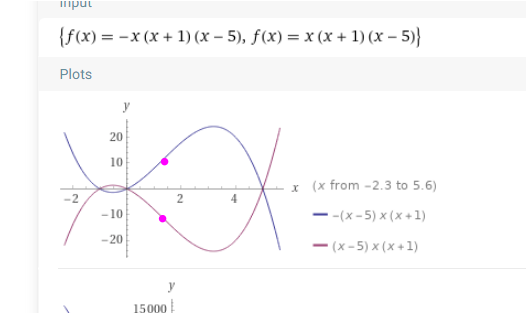
haben beide bei x = 4/3 ihren einzigen Wendepunkt . Aber bei der einen Fkt ist dort die Stelle mit der größten ,bei der anderen Fkt die mit der kleinsten Steigung .
Und es gibt bei der einen , die eine maximale Steigung hat , keine Stelle mit einer minimalen Steigung , der Wert geht gegen unendlich und das ist keine Zahl
.
Betragsmäßig sind aber beide gleich groß , in diesem Fall 31/3
Nein. Die Funktion
f(x) = x³ hat zum Beispiel gar keinen Punkt, wo sie
am stärksten steigt.
Ableitungen sind keine Punkte, sondern Funktionen.
Die zweite Ableitung ist eine Funktion. Wie kann eine Funktion ein Punkt sein?
Ja, ich meine es in etwa so „steigt/ fällt eine Funktion am Wendepunkt am meisten?