Integrale (Flächeninhalt zwischen zwei Graphen) - Wo liegt mein Fehler?
Hallo, ich habe ein paar Fragen:
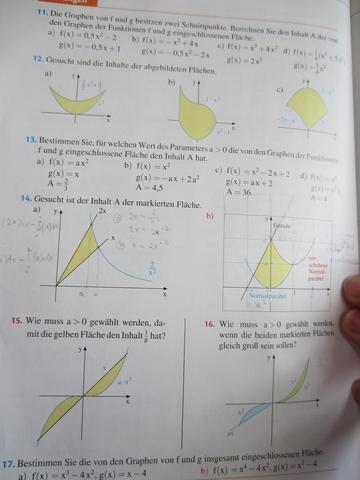
zu 11a) Ich kommen auf 4 verschiedene Ergebnisse (siehe Anhang = Fotos). Wo liegt mein Fehler? Eigentlich müsste es doch das Selbe sein, ob ich die Integrale (= Flächeninhalte) einzeln ausrechne und dann am Ende den kleineren Wert vom Größeren subtrahiere oder, ob ich die Gleichungen voneinander subtrahiere und dann davon das Integral berechne (SUMMENREGEL): I f(x) dx - I g(x) = I (f(x)-g(x)) dx (?) ; I = Integralzeichen
auch bei 11d kommen bei mir bei den beiden Mehoden unterschiedliche Ergebnisse raus. ?
Und könnte mir bitte jemand erklären, wie ich das Parameter a bestimme (Nr.13 u. 15)?
Ist Nr.17 einfach wie Nr.11 zu bearbeiten?
Dankeschön, dass du dir das hier wenigstens durchliest bzw. dir sogar die Mühe machst mir zu antworten ! :)
LG Starli



2 Antworten
mal ein paar prinzipielle Anmerkungen zum Thema fläche zwsichen 2 funktionen:
bestimme alle schnittpunkte der 2 funktionen miteinander, genauer die zugehörigen x werte.
bestimme alle x bei denen f(x) eine nullstelle hat (also f(x)=0) ist.
bestimme alle x werte für die g(x)=0 ist.
nun hast du ne menge an x werten, die du nun aufsteigend sortierst.
Sagen wir beispielhaft, die gefundenen x wete wären
x1,x2,x3,x4
um nun die fläche zwischen den funktionen zu bestimmen, berechnest du nacheinander die integrale zwischen den 2 funktionen von x1 nach x2, x2 nach x3 und x3 nach x4 und addierst die.
zu der berechnung eines einzelnen dieser "differenzintegrale":
Korrekt gesprochen müsstest du dir überlegen, welche der beiden Funktionen in dem intervall größer als die andere ist.
Macht aber nicht viel spaß und ist auch nicht immer so ersichtlich.
Darum mache es am besten wie folgt:
berechne integral f(x) in dem intervall.
berechner integral g(x) in dem intervall.
ziehe ersteres von letzterem ab.
nun könnte es ja sein dass f(x)>g(x) in dem ijntervall war.
darum nimm davon noch den betrag.
Wie sieht das in der praxis aus?
seien f(x),g(x) deine funktionen, F(x),G(x) deren stammfunktionen und a,b die grenzen des intervalls(b obere, a untere grenze).
Dann ist die fläche zwischen den 2 funktionen in dem intervall:
| (F(b)-F(a))-(G(b)-G(a)) |
Wenn du die 4 schritte oben der reihe nach machst, kommst du genau auf den ausdruck für das differenzintegral in dem intervall [a,b].
joa, der rest ist reine rechnerei.
Vergiss nicht, dass es hier in deinen beispielen um flächen geht. Von daher ist die aufteilung in die verschiedenen intervalle notwendig.
PS: mi ist übrigens nicht ganz klar wozu du f(0) und g(0) berechnest.
Leider habe ich gerade nicht genügend Zeit, um mir deine Rechenschritte anzuschauen, kann ich später gerne tun, wenn bis dahin nicht geklärt ist, wo dein Fehler liegt.
Ich kann dir nur folgenden Hinweis geben:
Wenn es darum geht, die Fläche zu berechnen, die der Funktionsgraph mit der x-Achse einschließt, dann musst du die Funktion "stückeln". Das heißt, du bildest Teilintegrale und addierst deren Beträge. Die Integralgrenzen der Teilintegrale sind dann jeweils benachbarte Nullstellen.
Falls aber in der Aufgabe nach dem Wert des Integrals gesucht wird, musst du über die gesamte Funktion integrieren. Hier darfst du dann nicht unterteilen; bzw. wenn doch, dann addierst du die Integralwerte und nicht die Beträge.
PS: Ich finde es lobenswert, dass du deine Lösung hochlädst. So sieht man, dass du keine Musterlösungen von uns haben möchtest, sondern dich selbst bemüht hast :-)