Integral positiv,negativ oder null?

Hallo,

ich schreibe Mittwoch eine Klausur und komme bei der Aufgabe nicht weiter wie man bestimmen soll (ohne Rechnung) ob das Intervall: positiv, negativ oder null ist.

Kann mir jemand weiter helfen ( unten ist auch eine Bsp Aufgabe woran man es mir erklären kann) oder ein YouTube Video link weiter empfehle wo das gut erklärt wird.

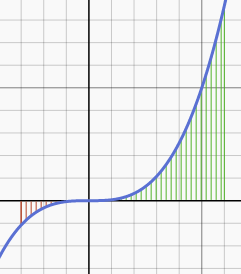
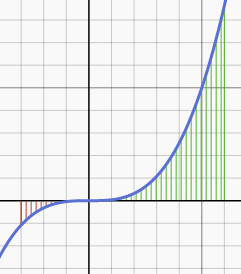
Intervall: -3;6 f(x)=x^3

danke !

Answer 1

[evtldocha]

Die Funktion ist symmetrisch zum Ursprung

$f\left(-x\right)=\ \left(-x\right)^3=-x^3=-f\left(x\right)$

Das Intervall [-3;6] ist nicht symmetrisch zum Ursprung. Für alle x<0 liegt die Funktion unterhalb der x-Achse (das Integral ist negativ) und für alle x>0 liegt die Funktion oberhalb der x-Achse (das Integral ist positiv). Da die Länge des Intervalls [0,6] größer als die Länge des Intervalls [-3;0] ist auch das positive Integral vom [0;6] größer als das negative Integral [-3;0]. Insgesamt ist das Integral positiv.

Oder auch zusammenfassend:

$\int_{_{-3}}^6x^3dx\ =\ \int_{_{-3}}^0x^3dx\ +\ \int_{_0}^3x^3dx\ \ +\ \int_{_3}^6x^3dx\ \$

Wegen der Punktsymmetrie der Funktion heben sich die beiden ersten Integrale auf der rechten Seite auf ( die Summe ist null) und es bleibt das dritte (positive) Teil-Integral übrig.

Skizze zur Veranschaulichung:

Comments

[Lolahammes06]

Dankeschön