ich soll folgendes Integral lösen 1/(wurzel(x³))?
mein Lösungsweg:
umschreiben zu (x³)^(-1/2).
Um eine Potenz zu "integrieren" muss man diese + 1 und den Term mal dem Kehrbruch nehmen, daher folgt:
2*(x³)^(1/2).
aber Laut integral rechner kommt -2/Wurzel(x) heraus...
wo wäre denn mein Fehler?
4 Antworten
Merke dir einfach, dass die "normale" Wurzel die 2. Wurzel ist. Möchte man die Variable x³ unter der Wurzel als Potenz schreiben, also ohne Wurzelzeichen, wandert die 2 aus der Wurzel in den Nenner des Bruches vom Exponenten und die Potenz von x in den Zähler des Exponenten.
So wird aus Wurzel(x³) zu x^(3/2)
Das ist immer dasselbe Verfahren, nur die Zahlen ändern sich. Steht der ganze Bums unter einem Bruchstrich, wird der Exponent von x negativ, wenn man die Variable x über den Bruchstrich schreibt.
Habe dir das in dem Bild nochmal möglichst selbsterklärend verdeutlicht.
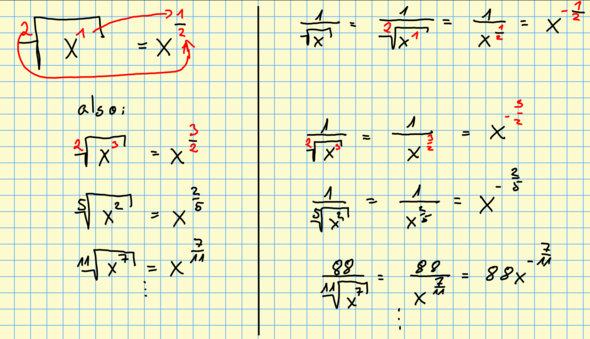
1/Wurzel x³=1/x^(3/2),
das vereinfachst du zu
x^(-3/2)
Das integrierst du nach der gelernten Regel:
f(x)=ax^n
F(x)=1/(n+1)*x^(n+1) + C
Wende doch mal Potenzgesetze an.
(a^b)^c = a^(b*c)
So, nun aber ;)
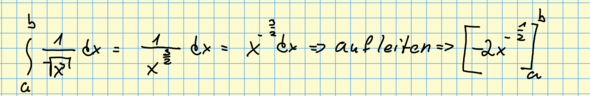
Danke für den Rechenweg!
Zwei Fragen und zwar:
- eine Wurzel ist doch umgeschrieben immer 1/2 bzw. -1/2 wenn diese im Nenner eines Bruches steht, wie kommt man hier auf -3/2?
das Ergebnis laut Integralrechner ist: "-2/Wurzel(x)" ist dies identisch mit -2x^(-1/2)
oh man, ich dachte immer das die Wurzel umgeschrieben generell "^1/2" ist und das z separat betrachtet wird...
kann man sagen, dass wenn im Bruch eine Wurzel im Nenner ist, dass:
wurzel(z) = z^-1/2
wurzel(z²) = z^-2/2
wurzel(z³) = z^-3/2
wurzel(z^4) = z^-4/2
stimmt, dies?