Ich brauche Hilfe in Mathe! Wie berechne ich eine Fledermausgaube (e-Funktion)?
Die Abbildung zeigt eine Fledermausgaube, sie 4m breit ist. Das obere Randprofil wird durch die Funktion f(x)= 2e^(1/8)x^2 für -2<x<2 modelliert.
a) Wie hoch ist die Gaube an ihrer höchsten Stelle?
b) An welchen Stellen ist das Profil am steilsten? Wie groß ist der Steigungswinkel?
c) Die Gaube besitzt ein parabelförmiges Fenster. Es ist 3 m breit und 1,5 m hoch. Wie lautet die Gleichung der Fensterparabel? Wie groß ist die Glasfläche?
d) Am Gaubenrand soll eine Antenne angebracht werden, deren Höhe 1m beträgt. Sie soll die Gaubenspitze nicht überragen. In welchen Bereich kann sie aufgestellt werden?
Ich danke euch im Voraus! :-)
1 Antwort
Ich glaube, dass Du die Formel falsch abgeschrieben hast.
2 * e^(1/8) * x^2 ergibt eine Parabel mit dem Faktor 2 * e^(1/8)
Eine Funktion, die ein Dach einer Fledermausgaube ergibt, sieht etwa so aus:
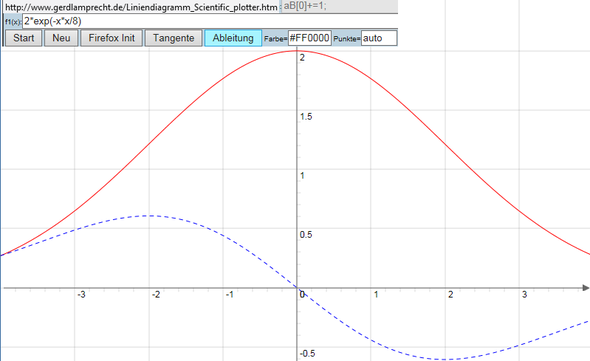
2*exp(-x*x/8) = 2 * e^(-x²/8)
http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm
siehe Bild
a) f(0) ausrechnen
b) mathematisch: max(f ' (x) ) im Bild das Maximum der blau gestrichelten Kurve
c) hört sich nach f2(3/2)=3/2 an mit f2(x) = a* x²
d) hört sich nach f(0)-f(x)=1 an
Achtung: c) könnte auch eine nach unten offene Parabel sein mit
f2(x)=2-a * x²