Höhe b = 1/2e...immer so beim Parallelogramm?
Hallo,
meine kleine Schwester muss ein Portfolio zu den Vierecken erstellen (8. Klasse). Da ich sehr gut bin, helfe ich ihr in Mathe. Nun habe ich gerade ein Parallelogramm konstruiert und eine "Entdeckung" gemacht, bzw. mir ist was aufgefallen.
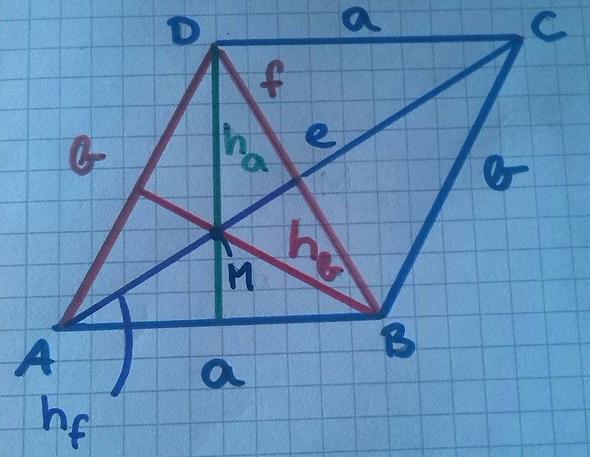
Und zwar: Wenn ich ha und hb - also die Höhen der Seiten - so konstruiere, dass sie sich schneiden, dann schneiden sie sich gemeinsam mit der Diagonale e des Parallelogramms in einem Punkt. Wenn ich nun auch die Diagonale f konstruiere, erhalte ich zwei Dreiecke, die meines Erachtens Gleichschenklig sind (in meiner Konstruktion, ich hänge euch ein Bild an). Nun fiel mir auf:Die drei Strecken schneiden sich im Punkt M (so nenne ich den jetzt), das ist doch der Schnittpunkt der drei Höhen eines Dreiecks (also Höge a, Höhe b und der Teil der Diagonalen e als Höhe f (hf nenne ich die jetzt mal).
Jetzt habe ich da dieses gleichschenklige Dreieck, das heißt - da e und b gleich lang sind und auch e und f sich gegenseitig halbieren -, dass hb = 1/2e = hf...
Ist das immer so oder habe ich nur eine "glückliche Konstruktion"?
Ich wäre dankbar für Antworten - das ist keine Hausaufgabe und auch meine Schwester muss das nicht wissen...mit Kommentaren wie "Mach' deine Hausaufgaben selbst" oder "Lern mal Mathe" oder so könnt ihr mir vom Halse bleiben, ich stehe auf 15 Punkten in Mathe.
Im Anhang wie gesagt die Konstruktion, hf ist ein Teil von der Diagonale e.
LG ShD
3 Antworten
Bist du sicher, dass du "Parallelogramm" und nicht "Rhombus" / "Raute" meinst? Bei einem Parallelogramm sind nur gegenüberliegende Seiten in jedem Fall gleich lang, nicht aber aneinandergrenzende.
Wenn du mit Höhen die Höhen durch einen Eckpunkt meinst und die Figur tatsächlich ein Rhombus sein soll, sind deine Überlegungen korrekt. (Gleichschenkliges Dreieck; siehe auch die Antwort von UlrichNagel)
Im Parallelogramm kannst du ja die "Höhen" beliebig hinsetzen, sie haben nicht wie im Dreieck einen bestimmten Punkt! Die Diagonalen trennen ja das Parallelogramm in 2 kongruente Dreiecke und sind gleichzeitig die Höhen darin, wie du unschwer erkennen kannst.
Dass die Diagonalen die Höhen sind, gilt allerdings nur im Rhombus, nicht im allgemeinen Parallelogramm.
na probiers doch aus
inwiefern "ausprobieren"? Wenn,dann müsste ich es beweisen.