Hilfe zur Matheaufgbe Motorradstunt?
Hi ich komme hier leider nicht mehr weiter kann mir jemand helfen?
Ein Stuntman wagt einen Motorradsprung über mehrere Autos. Der Absprung erfolgt nach Anfahrt über eine Rampe im Punkt P(0/ 1). Die anschließende Flugkurve des Motorrads wird durch die Funktion h mit h (x)= 0,25x - 0,013x2 + 1 modelliert. Eine Rampe zur Landung des Motorrads hat einen Neigungswinkel von 14° gegenüber der Waagerechten. Der Landepunkt soll in der Mitte dieser Rampe in 0,5 m Höhe über der Erdoberfläche erfolgen.
a) welche maximale höhe erreicht das motorrad?
b) wie lang ist der Sprung?
c)Der Winkel zwischen der Landerampe und der Flugkurve muss im Landepunkt kleiner als 3° sein. Ist diese Sicherheitsbedingung erfüllt?
Was zur Hölle? Wie soll man das bitte lösen?
2 Antworten
So sieht die Flugkurve aus:
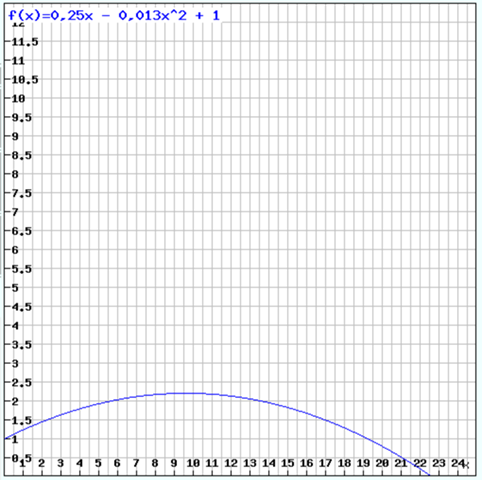
In wirklichkeit ist sie etwas flacher, da y- und x-Achse einen unterschiedlichem Maßstab haben.
Das Maximum dieser Flugkurve erhält man mit einer Kurvendiskussion:

Ergebnis a):
Das Motorrad erreicht eine maximale Höhe von 2,202 m
b) Der Sprung ist zu Ende, wenn eine Höhe von 0,5 erreicht wird. Die restlichen Angaben zur Rampe dienen nur zur Verwirrung. Also:
0,5 m = 0,25x - 0,013x2 + 1
da machen wir eine quadratische Gleichung draus:
- 0,013x^2 + 0,25x + 0,5 = 0
0,013x^2 - 0,25x - 0,5 = 0
x^2 - 19,23x - 38,46 = 0
und die lösen wir jetzt mit quadratischer Ergänzung, pq-Formel oder mit der Mitternachtsformel.
Mir ist die pq-Formel am liebsten:

minus 1,827 können wir vergessen, da das Motorrad ja nicht rückwärts fliegt.
Ergebnis: Nach 21,057 m kommt das Motorrad auf der Rampe auf. (Das entspricht auch dem Graphen oben)
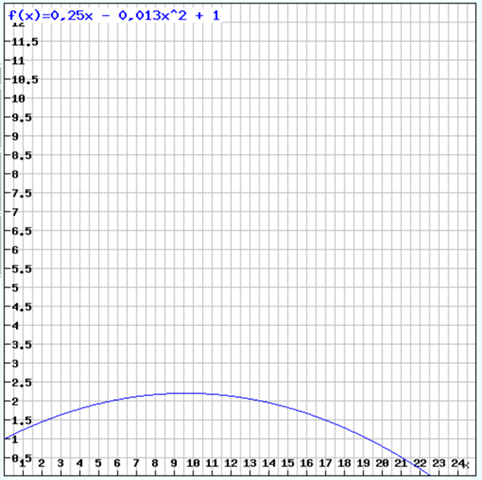


Maximum bestimmen,
x für f(x) = 0,5 bestimmen.
Warum der Winkel der Rampe gegeben ist erschließt sich mir nicht.
Den Winkel hätte man über den Arkustangens und über die Ableitung leicht selbst berechnen können.