Hilfe bei Mathe/ Extremwertaufgabe
Hallo, ich schreibe in wenigen Tagen Klausur und komme mit diesem Thema wirklich sehr schlecht zurecht und besonders diese Aufgabe bereitet mir Kopfzerbrechen:
Ein Unternehmen verkauft T-Shirts zum Preis von 15€ und macht dabei 8€ Gewinn pro T-Shirt. Bei diesem Preis verkauft das Unternehmen täglich 500 T-Shirts. Eine Marktuntersuchung hat ergeben, dass bei einer Preissenkung mehr T-Shirts verkauft werden können. Man geht davon aus, dass pro Euro Ermäßigung 80 T-Shirts mehr pro Tag verkauft werden. Berechne um wie viel Euro man den Preis reduzieren sollte, damit der Gewinn am größten ist.
Ich habe bis jetzt : G=500*8€=4000€
x=Anzahl der verkauften T-shirts y=Gewinn je T-shirt G=x*y
Extr.bed.: G(x,y)=x*y Nebenbed.: x=500+80a; a=Absenkung des Preises , y=8-a Zielfunktion: G=(500+80a)(8-a)
Und genau ab diesem Punkt komme ich nicht weiter..brauche ja eigentlich die 1. Ableitung habe jedoch keine Ahnung wie ich die bilden soll.
Kann mir jemand helfen?
4 Antworten
Na, also wenn du diese Vorüberlegungen anstellen konntest, dann frage ich mich, wieso du an so einer wirklich einfachen Multiplikation zweier Klammerinhalte scheiterst ...?
Multipliziere jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer:
( 500 + 80 a ) * ( 8 - a ) = 500 * 8 - 500 * a + 80 a * 8 - 80 a * a
= - 80 a ²+ 140 a + 4000
Bei mir scheitert es immer halt immer an den simplen Dingen -.- Danke Sehr, jetzt stimmt auch das Ergebnis !
Kannst doch einfach ausmultiplizieren. Ich würde aber gar keinen Faktor a einführen, sondern es so machen:
Ein Shirt kostet in der Herstellung also 7 €, da man bei 15 € 8 € Gewinn macht.
G = (P-7€) * N mit G = Gewinn, P = Verkaufspreis, N = Anzahl der verkauften Shirts
Außerdem weiß man, dass pro Euro weniger 80 Shirts mehr verkauft werden, also:
N(15€) = m * 15 € + b = 500 Shirts
N(14 €) = m * 14€ + b = 420 Shirts
Daraus lässt sich eine Geradengleichung (da lineare Zunahme der Anzahl bei Preissenkung) aufstellen:
N(P) = -80 1/ € * P +1700
Das kann man nun in die Gewinnfunktion einsetzen:
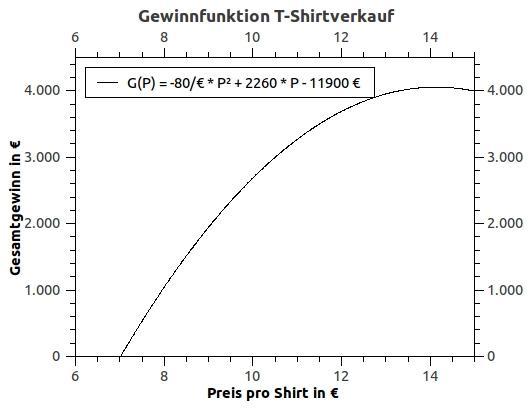
G (P) = (P-7€) * N = (P-7€) * (-80 1/€ * P +1700)
= -80/€ * P² + 1700P + 560P-11900 €
= -80/€ * P² + 2260 * P - 11900 €
Das leiten wir jetzt ab und setzen es 0, um das Maximum zu berechnen:
G ' (P) = -160/€ * P + 2260 = 0
160/€ * P = 2260
P = 14,125 €
Prüfen, ob es ein Maximum ist mit Hilfe der 2. Ableitung:
G ' ' (P) = -160/€ < 0, also ja, ist ein Maximum.
Den größen Gewinn erhält man also bei einem Preis von 14,125 €, also sollte man den Preis um 0,875 €, also ungefähr 88 cent reduzieren.
N(14 €) = m * 14€ + b = 580 Shirts muss das natürlich heißen! Die Geradengleichung ist aber wieder richtig
Du könntest die Klammern auflösen (binomische Formel und so), dann solltest du das ganz einfach ableiten können.
Genau da liegt ja das Problem^^ ich habe keine Ahnung wie ich diese Klammern auflösen soll. 3. Binomische Formel war auch mein Gedanke allerdings kam ich komischerweise auf ein Ergebnis von 4000-80a, was wiederrum keinen Sinn ergeben würde , oder?
Du kannst als erstes die Klammer auflösen indem du jeden Wert mit dem anderen berechnen kannst!
Als Ansatz dafür gebe ich dir mal die binomischen Formeln:
(a+b)²= (a+b)(ab) = a² + 2ab + b² (a-b)² = (a+b)(a-b) = a² - 2ab + b² (a+b)(a-b)= a² - b²
Soweit zu den Binomischen Formeln und wie sie gelöst werden! Vielleicht kommst du ja so drauf...
Da es sich bei dir jedoch nicht um eine binomische Formel handelt, da die Werte in den Klammern unterschiedlich sind, gebe ich dir ein anderes Beispiel mit einer ähnlichen Aufgabe wie deiner:
(5a+2b)*(4c-3d)= 5a *4c + 5a *-3d + 2b *4c + 2b *-3d
Jetzt dürfte klar sein, wie man eine solche Klammer löst!
Nun weiter zu deiner Extremwertaufgabe:
hast du die Klammer richtig gelöst, kommt für G = -80a² + 140 a + 4000 raus!
Die Ableitung bildest du, indem du von jedem Buchstaben an dem eine Potenz steht eine Zahl abziehst und die ursprüngliche Zahl mal dem Faktor nimmst, der vor dem Buchstaben steht: z.B.: P = 40 x² - 30 x - 20 Die Zahlen bei denen kein X oder a oder was auch immer steht FALLEN WEG!!! Zum Folgenden: dieses Zeichen "^" heißt HOCH! --> x^2 = X² Die erste Ableitung von dieser Funktion ist P'(<-- 1. Ableitung wird immer mit einem Strich gekennzeichnet, die zweite mit '' etc...)= 402x^2-1 - 30 * 1 * x ^1 - 1
--> P' = 80 x - 30 , da die Potenz 1-1 = 0 ist fällt hier das X weg. die zweite Ableitung P'' wäre dann so: P'' = 80
Um deine Extremstelle für "a" zu berechnen bildest du also jetzt von G = -80a² + 140 a + 4000 die erste Ableitung!
G' = -802a + 140 --> -160 a + 140 Diese Ableitung setzt du mit 0 gleich. d.h.: 0 = -160 a + 140 und dann berechnest du einfach nur noch a
Ich hoffe ich konnte dir helfen und auch meine Hilfe für nicht-mathe-profis verständlich genug beschreiben :)