Halbwertszeiten?
Hi,
ich möchte berechnen, nach wie vielen Jahren nur noch 5 % eines radioaktiven Stoffs vorhanden ist.
In diesem Fall Cäsium 134
Halbwertszeit: 2,06 Jahre
t = log(0,05) / log(1-0,0206) ≈ 143,92
Frage:
Spielt bei dieser Berechnung die Massezahl des Elements (134) irgendeine Rolle?
Danke
3 Antworten
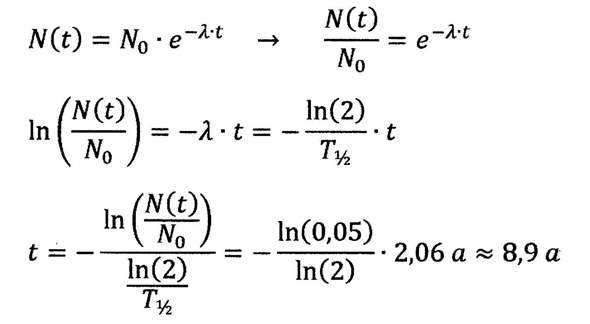
LG H.

Nein, Halbwertszahl ist nicht durch Massenzahl bedingt. (Meinst du das?)
Die Massenzahl ist nötig, um das Isotop festzulegen. Verscheidene Isotope haben unterscheidliche Halbwertszeiten und sind evtl. sogar stabil.
(1/2)^(x/2,06) = 0,05 liefert bei mir 8,9 Jahre?
Ich weiß nicht, wie du darauf kommst. Meine Berechnung ist doch korrekt.
Check:
p = (1 - Halbwertszeit)^t
= (1 - 0,0206)^143,92
≈ 0,05 = 5 %
Wo soll mein Ansatz falsch sein?
der Ansatz ist merkwürdig. Wenn die Halbwertszeit 2 Jahre ist, sind nach 10 Jahren 5 Halbwertszeiten vergangen. (1/2)^5 = 0,03, da liegst du schon unter 5%
Ok, könntest du deinen Ansatz erklären?
Ja, das meine ich. In der Aufgabenstellung wird das immer wieder erwähnt. Ich habe aber nicht verstanden, wozu das nötig sein soll. Es dient also wahrscheinlich nur der Verwirrung.