Funktionsgraph bei dem die 1. Und 2. Ableitung negativ sind?
Ich muss für die schule einen Funktionsgraphen bei dem die 1. Und 2. Ableitung immer negativ sind skizzieren, ich weiß aber nicht wie das geht. Kann mir jemand von euch helfen?
Danke schon mal im vorraus! :)
4 Antworten
Inzwischen habe ich Deine ausführliche Aufgabenstellung gelesen.
Dank GeoGebra habe ich Dir mal eine Zeichnung erstellt: der Graph geht abwärts und ist rechtsgekrümmt. Bei der Funktion habe ich mich ganz schwer von DepravedGirl inspirieren lassen (mir ist nämlich auch keine andere Funktion eingefallen). Die konkrete Funktion spielt aber keine Rolle.
Wenn Du nun an irgendeiner Stelle eine Tangente an den Graphen von f [ bzw. von f´] zeichnest und per Steigungsdreieck die Steigung bestimmst, wirst Du feststellen, dass dies genau der Funktionswert von f´ [bzw. f´´] an dieser Stelle ist.
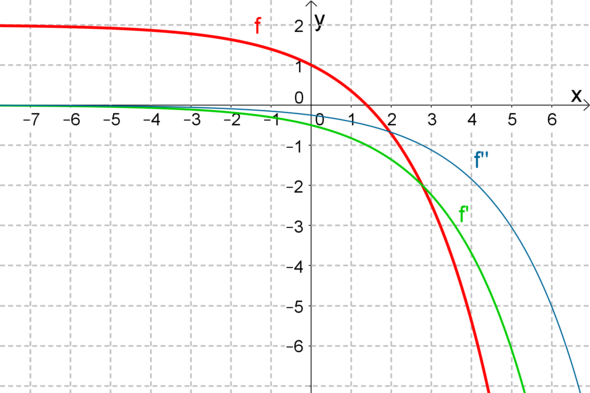
f(x) = -5x^2
f'(x) = -10x
f''(x) = -10
Bei höher-gradigen Funktionen wird's etwas schwer, da mehr Scheitelpunkte vorhanden sind.
Wieso ist -10x negativ? Nur weil da ein "-" steht? Und was ist, wenn x=-3 ist?
Wie zeichne ich den Graph der 2. Ableitung? Und wie kommt man auf diese Funktion? :/
Bei der Funktion y = f(x) = - (e ^ x) ist die 1-te Ableitung UND die 2-te Ableitung immer negativ, sowohl für negative als auch für positive Werte von x
Gibt es auch noch eine andere als eine mit e ? Das hatten wir nämlich noch nicht xD :/
Mir fällt keine andere ein, sorry. Vielleicht kennt jemand anderes noch eine.
negative erste Ableitung bedeutet: der Graph fällt
negative zweite Ableitung bedeutet: der Graph ist rechtsgekrümmt.
Langt das als Hinweis?
Ne langt nicht, kannst du vielleicht mal ein Beispiel machen? Ich verstehe es leider nicht :/
Wenn ich die Aufgabe richtig verstanden habe, brauchst Du ja keine konkrete Funktion anzugeben/zu finden, sondern sollst "nur" einen Graphen skizzieren.
Also zeichnest Du eine Linie, die (zumindest auf Deinem Bild) ausschließlich nach unten läuft UND das außerdem auch noch in einer Rechtskurve.
Langt's nun?
Ich bin davon ausgegangen, dass Ihr den Zusammenhang "Negative zweite Ableitung = Rechtsgekrümmter Graph" hattet; sonst würde die Aufgabe für mich keinen Sinn machen.
Danke für die schöne Vorlage für eine Funktion!!