Frage zu Mathematik zum Thema Steigung und Steigungswinkel?
Ich habe ein Arbeitsblatt(siehe Bild) und da wurde ich darauf hingewiesen, dass bei der Geraden h, wo Alpha 3= 22Grad steht , man 22 von 180 abziehen müsse also 158Grad, um dann mittels diesen Wertes über tangens die Steigung der Geraden zu ermitteln. Jetzt ist meine Frage, ob das dann auch bei den anderen Geraden der Fall ist, also bei Gerade g 63Grad(180-117) und bei Gerade f 135 Grad?
Bei den drei anderen Graphen dementsprechend g = 56,3 Grad, bei f 153,4 Grad und bei h dann 141,3 Grad.
4 Antworten
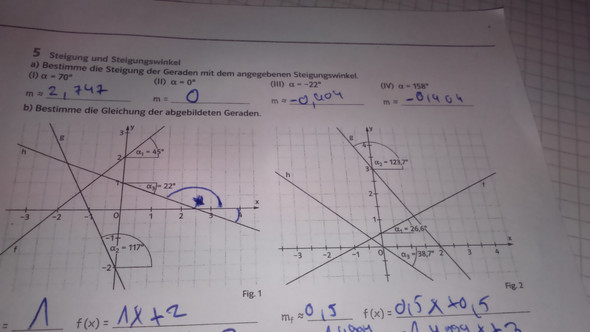
Figur 1 und Figur 2
da kannst du die Winkel nehmen, wie sie da stehen und selber + bzw -
beim Ergebnis setzen; ich denke, du siehst selbst, ob die Gerade steigt oder fällt.
bei den beiden g musst du 180-117 bzw 180-123,7 nehmen.
Sonst nachfragen.
Das liegt daran, dass der Winkel math. Definiert ist. Er beginnt auf der pos. x-Achse und läuft gegen den Uhrzeigersinn. Du hättest statt 158° auch -22° nehmen können, da der Winkel ja sozusagen unter der x-Achse liegt.
Bei g nein, da der Winkel zwischen x-Achse und Geraden liegt. Bei f sind's auch wieder 45°
Solange wir nur bei Fig. 1 sind.
Ach noch einen Kleinen Tipp, Einheitskreis mal genauer anschauen ;)
g und f sind es die angegebenen Winkel bei h entweder -38,7° oder eben die 141,3° .
Der Steigungswinkel einer Geraden wird von einer Parallen zur der postiven x-Achse aus gegen den Uhrzeigersinn gezählt.
Bei α1 und α2 ist die Zählrichtung gegen den Uhrzeigersinn, bei α3 im Uhrzeigersinn. Also müßte dort eigentlich stehen α3 = -22°. Um auf einen postiven Winkel zu kommen, addiert man 180° >> α3 = -22° + 180° = 158°
Indem Du α3 = 22° von 180° abziehen sollst, machst Du genau das Gleiche, du kehrst den Winkel (+22°) ins Negative: α3 = 180° - (+22°) = 180° + (-22°) = 158°
An der Schnittstelle der Geraden h mit der x-Achse wird das deutlicher: Ausgehend von der Waagerechten gehst Du gegen den Uhrzeigersinn, bis Du die Gerade triffst: Ergebnis 158°
Nein. Bei h muss jeweils der Winkel angepasst werden, bei g und f nicht.
Bei der linken Seite: Bei der Gerade h ist (von der positiven x-Richtung aus gesehen) der Winkel nach unten angegeben, daher muss man mit 180°-22° rechnen bzw. mit -22°.
Dementsprechend erhält man als Steigung:
tan(180°-22°) = tan(158°) ≈ -0,404
bzw.
tan(-22°) ≈ -0,404
Warum man das machen muss, wird dir evtl. klar, wenn du dir die beiden Geraden im angehängten Bild ansiehst. Diese haben offensichtlich unterschiedliche Steigung.
Bei der Geraden g ist die Steigung tan(30°) ≈ 0,577.
Bei der Geraden h hingegen ist der Steigungswinkel 180°-30° = 150°, da der 30° in die falsche Richtung (nämlich nach unten, statt nach oben) angegeben ist. Die Steigung ist dementsprechend tan(150°) ≈ -0,577.
[Alternativ kann man bei h auch, statt mit dem Steigungswinkel 150° zu rechnen, dem 30° ein negatives Vorzeichen verpassen: tan(-30°) ≈ -0,577]

Danke, wäre es dann bei Figur zwei so, dass bei den Geraden g und f die Winkel bleiben und bei h wäre es dann 141,3 Grad?