Entfernung Mittelpunkt -> Ecke beim gleichseitigen Dreieck?
Hi, wie berechnet man die Entfernung vom Mittelpunkt eines gleichseitigen Dreiecks, der Seitenlänge a, von einer der Ecken?
3 Antworten
Im Mittelpunkt schneiden sich h_A und h_B
In einem gleichseitigen Dreieck haben alle Winkel 60 °
Die Steigung der Geraden die h_A bildet hat hat den Steigungswinkel 30 °
und die Steigung der Geraden die h_B bildet hat den Steigungswinkel - 30°
m = tan(Steigungswinkel)
Nun die Geradengleichungen aufstellen :
1-te Gerade :
g _ 1 = 0.577350269 * x
2-te Gerade :
m = - 0.577350269
Punkt (a | 0)
0 = - 0.577350269 * a + b
b = 0.577350269 * a
g _ 2 = - 0.577350269 * x + 0.577350269 * a
Schnittpunkt der beiden Geraden :
0.577350269 * x = - 0.577350269 * x + 0.577350269 * a
2 * 0.577350269 * x = 0.577350269 * a | : 0.577350269
2 * x = a
x = a / 2
in g _ 1 einsetzen :
0.577350269 * (a / 2) = tan(30°) * a / 2
Abstand
zwischen dem Punkt (0 | 0) und dem Punkt (a / 2 | tan(30°) * a / 2) mit
der Abstandsformel zwischen zwei Punkten ausrechnen (Internet) :
d = √((a / 2) ^ 2 + (tan(30°) * a / 2) ^ 2)
tan(30°) ^ 2 = (1 / 3)
d = √((1 / 4) * a ^ 2 + (1 / 12) * a ^ 2)
d = √((3 / 12) * a ^ 2 + (1 / 12) * a ^ 2)
d = √((4 / 12) * a ^ 2)
d = a / √(3)
--------------------------------------------------------------------------------------------------
Eine völlig andere Herleitung :
In einem gleichseitigen Dreieck gilt folgendes :
3 * a = h * √(12)
also
h = 3 * a / √(12)
außerdem betragen alle Winkel 60 °
Wenn du nun a / 2 und Winkel (60 ° / 2) nimmst und auf das rechtwinklige Dreieck überträgst, dann erhältst du :
Gamma = 90 °
b = a / 2
Alpha = 30 °
a = b * tan (Alpha)
c = a / sin (Alpha)
Beta = 90 ° - Alpha
a = (a / 2) * tan(30°)
c = (a / 2) * tan(30°) / sin(30°)
Beta = 60 °
tan(30°) / sin(30°) = 2 / √(3)
c = (a / 2) * 2 / √(3) = a / √(3)
c = a / √(3)
Da ich den Abstand oben d genannt hatte also :
d = a / √(3)
Es bleibt also dabei, die Entfernung des Mittelpunktes zu einem Eckpunkt beträgt im gleichseitigen Dreieck d = a / √(3)
Schau Dir mal dieses Dreieck an. Hilft Dir das was?
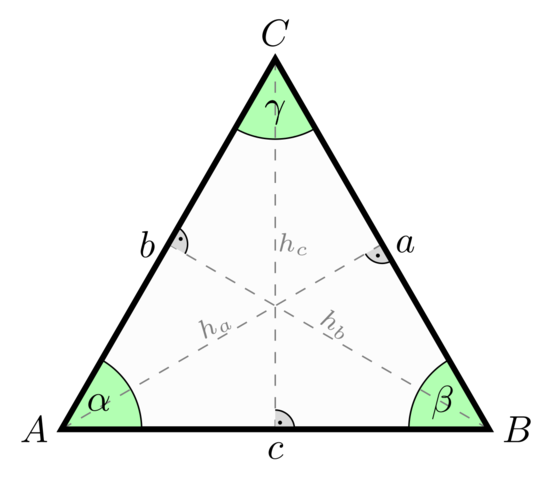
Wie konstruierst Du den Mittelpunkt? Hat was mit den Senkrechten auf der halben Seite zu tun.
Heißt das, Du kannst es nicht ausrechnen oder Du weißt nicht, wie man dazu kommt?
mit sqrt(3) / 2 * a
aber ich weiß nicht weiter.