Dreisatz - Lösungsweg?

36 Arbeiter errichten eine Mauer bei 10-Stündiger Arbeitszeit in 15 Tagen. Wie lange brauchen 27 Arbeiter, wenn sie nur 8 Stunden täglich arbeiten.

Erbitte Hilfe :)

Answer 1

[Volens]

Da braucht man gleich einen Fünfsatz.

1. Satz     36 Arb.   ≙   10  Std.    ≙       15 Tg.       weniger Arb. = mehr Zeit
2. Satz       1 Arb.   ≙   10 Std.     ≙     540 Tg.        
3. Satz       1 Arb.   ≙     1 Std.     ≙    5400 Tg.      mehr Arb. = weniger Zeit
4. Satz       1 Arb.   ≙     8 Std.     ≙      675 Tg.
5. Satz     27 Arb.   ≙     8 Std.     ≙      25 Tage                                          

Bei der umgekehrten Proportionalität multipliziert man auf einem Feld mit dem Faktor, mit dem man ein anderes Feld dividiert. Eins von den dreien lässt man immer in Ruhe.

http://dieter-online.de.tl/Dreisatz-_-F.ue.nfsatz.htm

Woher ich das weiß: eigene Erfahrung – Unterricht - ohne Schulbetrieb

Answer 2

[Nadelwald75]

Hallo luured,

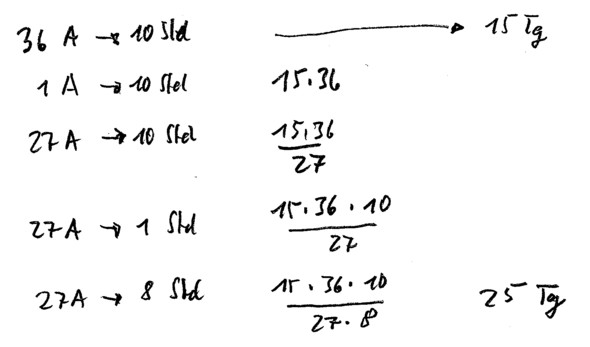
das ist ein "Fünfsatz". Je weniger Arbeiter, desto mehr Tage und umgekehrt, je weniger Stunden am Tag, desto mehr Arbeitstage und umgekehrt. Du gehst immer auf 1 zurück und dann wieder auf die neue zahl, schreibst das als Bruch und rechnest erst zum Schluss alles aus (siehe Bild).