Beweis mithilfe von vollständiger Induktion bei schwieriger Produktzeichen-Gleichung. Nächste?
Aufgabe:
Ich möchte folgende Aussage mithilfe von vollständiger Induktion für alle n≥1 beweisen:
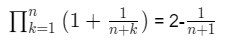
Ich habe bereits den Induktionsanfang, die Induktionsvoraussetzung und Induktionsbehauptung bestimmt. Da hat alles geklappt. Doch beim Induktionsschluss bin ich bei folgender Gleichung auf Probleme gestoßen:
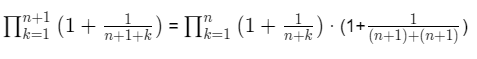
Erste Frage ist ob die Gleichung beim Induktionsschluss so richtig ist oder ob mir da bereits beim aufstellen der Gleichung ein Fehler unterlaufen ist. Und falls sie korrekt ist, wie man diese nun richtig auflöst, da bei mir immer sinnlose Gleichungen rauskommen. Würde mich über Hilfe sehr freuen.
3 Antworten

Ich würde in der zweiten Gleichung erst mal den Laufindex k um 1 erhöhen, damit man auf die Formel für n greifen kann:
Produkt( k; 1; n+1 ) ( 1 - 1/(n+1+k) ) =
Produkt( k; 2; n+2 ) ( 1 - 1/(n+1+k-1) ) =
Produkt( k; 2; n+2 ) ( 1 - 1/(n+k) ) =
Produkt( k; 1; n ) ( 1 - 1/(n+k) ) / (1+1/(n+1)) * (1+1/(2n+1)) * (1+1/(2n+2))
Die Faktoren rechts kommen von k=1, n+1 und n+2.
Nach Voraussetzung hat man nun
( 2 - 1/(n+1) ) / ( 1 + 1/(n+1) ) * ( 1 + 1/(2n+1) ) * ( 1 + 1/(2n+2) ) =
2 - 1/(n+2)

Du hast Dich beim Umformen vertan:
Links laufen die Nenner von n+2 bis 2(n+1). Rechts hast Du Nenner von n+1 bis 2n und noch ein 2(n+1).
Du musst rechts also noch durch 1+1/(n+1) teilen und den Faktor 1+1/(2n+1) explizit stehen lassen.

Da fehlt im nenner vom faktor ganz rechts noch eine +1