Berechnung: Unterschied einseitig offene, beidseitig offene Orgelpfeifen?
Ich muss als Hausübung die Frequenz einer Orgelpfeife berechnen. Einmal für eine einseitig offene und einmal für eine beidseitig offen. Meine Frage ist, was bei der Berechnung der Unterschied ist. Ich würde mich über Formeln oder eine ausführliche Erklärung als Antwort freuen.
Angabe:
Die Länge einer C-Orgelpfeife beträgt 26.9 cm (Mündungskorrektur berücksichtigt). Berechne die Frequenzen und die Wellenlängen der Grundschwingung, der 1. 2. und 3. Oberschwingung für:
- eine beidseitig offene Pfeife
- eine Pfeife mit einer Seite offen und einer Seite geschlossen
Überprüfe, ob die Grundschwingung wirklich ein C ist (Internet).
2 Antworten
Hallo Marvelfan,
zur Aufgabenstellung:
Die halte ich für einen Otto-Normal-Schüler für nicht lösbar, es sei denn, der gesamte Stoff wurde im Unterricht eingehend durchgearbeitet.
"Überprüfe, ob die Grundschwingung wirklich ein C ist..."
Orgelregister haben als Zusatz zu ihrem Namen die Länge ihrer größten Pfeife in Fuß. Die größte (tiefste) Pfeife ist zumeist ein c. 'Fuß' ist eine alte Längeneinheit, 1 Fuß = 32 cm. Die Pfeifen für alle Töne c haben also die Länge von 32 cm, oder ein Vielfaches davon (tiefere Oktavlagen), oder einen entsprechenden Bruchteil davon (höhere Oktavlagen).
Dies ist jedoch die theoretische Länge. Da die in der Pfeife schwingende Luftsäule nicht direkt am Ende der Pfeife endet, klingt eine Orgelpfeife etwas tiefer. Sie muss für die gewünschte Tonhöhe also etwas kürzer gebaut werden, die Differenz nennt man Mündungskorrektur.
Die Mündungskorrektur entspricht ungefähr 5/3 des Pfeifendurchmessers.
Die Aufgabenstellung ergibt eine Mündungskorrektur von 32 cm - 26,9 cm = 5,1 cm.
Daraus lässt sich ein Pfeifendurchmesser errechnen: 5,1 cm : 5/3 = 3,0 cm
Ein solcher Durchmesser ist sehr plausibel, demzufolge klingt die (offene) Pfeife mit dem Ton c2, wenn sie einen Durchmesser von 3 cm hat.
Fazit: Ja, die Grundschwingung ist tatsächlich ein c, und zwar c2.
Kleiner Trost an dieser Stelle: Wenn Du das verstanden hast, hast Du den schwierigsten Teil hinter Dir.
"Berechne (...) die Wellenlängen der Grundschwingung..."
Hier wird's einfacher, denn hier spielt die Mündungskorrektur keine Rolle mehr: Es wird die schwingende Luftsäule betrachtet, nicht mehr der Pfeifenkörper.
Zur Sprachregelung:
Der Orgelbauer oder Organist spricht von einer offenen und einer gedeckten Orgelpfeife.
Der Physiker spricht von einer beidseitig offenen Pfeife und einer Pfeife mit einer Seite offen und einer Seite geschlossen und meint damit dasselbe.
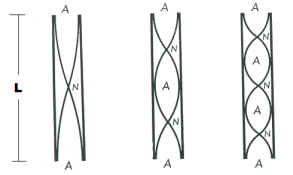
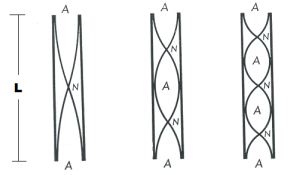
Wie diese Grafik für die offene Pfeife zeigt, entspricht die Wellenlänge des Grundtones der Länge der Luftsäule.
1. Oberton: Luftsäule mal 1/2 --> 32 cm x 0,5 = 16 cm
2. Oberton: Luftsäule mal 1/3 --> das rechnest Du 😉
3. Oberton: Luftsäule mal 1/4 --> s. o.
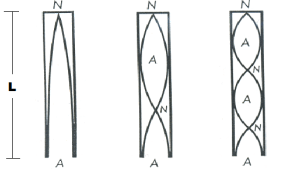
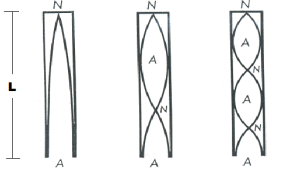
Diese Grafik zeigt die Wellenlängen in geschlossenen (gedeckten) Pfeifen. Die Wellenlängen haben die doppelte Länge von denen in offenen Pfeifen. (Deshalb klingen gedeckte Pfeifen eine Oktave tiefer.)
Der nächste Schritt ist einfach: Alle Werte werden verdoppelt.
Alles frisch? Dann geht's gleich weiter:
"Berechne die Frequenzen (...) der Grundschwingung..."
Hier kommt die Formel, nach der Du oben gefragt hast. Da die Mündungskorrektur auch hier keine Rolle spielt und keine Temperatur vorgegeben ist, ist sie recht einfach. Für offene Pfeifen:
L = Länge (32 cm) / v = Schallgeschwindigkeit (343 m/s) / f = Frequenz
Für die Länge:
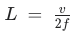
Für die Frequenz:
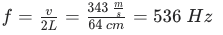
Diese Frequenz für das 'c' weicht geringfügig von 'handelsüblichen' Tabellen für Tonfrequenzen ab, da das alte Maß 'Fuß' variabel war, und in aller Regel nicht präzise 32,0 cm. (Für den Ton c'' auf dem modernen Klavier müsste man einen Wert von 32,8 cm für 1 Fuß annehmen.)
Analog zu den Wellenlängen:
1. Oberton: 536 Hz x 2
2. Oberton: 536 Hz x 3
3. Oberton: 536 Hz x 4
für gedeckte Pfeifen:
Gedeckte Pfeifen klingen eine Oktave tiefer.
Wellenlänge: alle Werte mal 2
Frequenz: alle Werte geteilt durch 2
Alles klar? Falls Du Fragen hast, immer zu! 😉
LG
Arlecchino
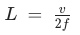
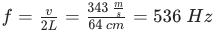
Hallo Marvelfan576!
Die sogenannten "Gedackt"-Pfeifen klingen eine Oktave tiefer, als die offenen. Mehr dazu: https://de.wikipedia.org/wiki/Gedackt
Gruß Friedemann