Berechnung an Figuren Mathe Würfel/Raumdiagonale/Winkel?
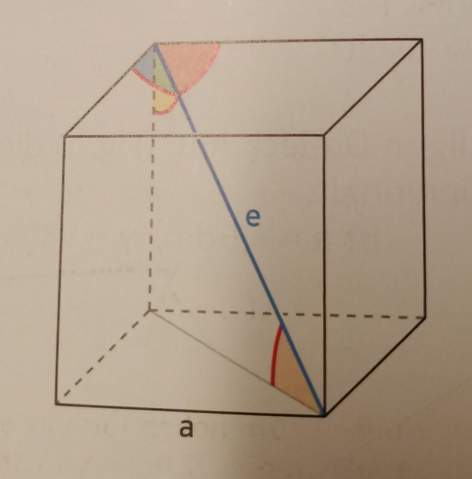
Begründe:Die drei eingezeichneten Winkel,die die Raumdiagonale e mit den Würfelkanten einschließt, sind gleich groß. Berechne die Größe dieser Winkel .
Wie berechne ich das?
Danke im Voraus ;)
5 Antworten
Also, der gelbe und orangene Winkel sollten einfach sein, da sie zu einem gleichschenkeligen, rechtwinkligem Dreieck gehören.
Hast du dazu selbst schon einen Lösungsansatz?
Dann helfe ich dir weiter.
Tipp: Ein - planes - Dreieck hat immer die Winkelsumme 180°.
Versuch Dir vorzustellen, Du guckst schräg von links drauf. Dann siehst Du, dass e zusammen mit zwei Seiten ein rechtwinkliges und gleichzeitiges Dreieck ist.
Ab da wird's einfach ;-)
[Klugscheissermodus]gleichseitig, nicht gleichzeitig [/klugscheissermodus]
Funktioniert leider nicht. Die andere Kathete ist eine Flächendiagonale (wie die eingezeichnete).
a) Symmetriegründe
b) e bildet mit der eingezeichneten Flächendiagonalen und der senkrechten Kante hinten links ein rechtwinkliges Dreieck. (Kannst du begründen, wieso?) Dann Pythagoras.
Die Größe der Winkel folgt aus der Definition des Sinus oder Cosinus im rechtwinkligen Dreieck. (Auflösen nach dem Winkel)
Wenn du de Würfel um die E-achse drehst, dann kannst ihn wieder in it der ursprünglichen Figur in Deckung bringen.
wenn du noch die Diagonalen BE und BG einzeichnest, siehst du , dass bei allen 3 Winkeln gilt:
sin(winkel) = Diagonale/e
Gleichschenklig?