Berechne die Geschwindigkeit eines Punktes am Erdäquator?
Die Aufgabe lautet: Berechne die Geschwindigkeit eines Punktes am Erdäquator. Der Erdradius misst 6370km.
hat irgendjemand eine Ahnung? Bitte mit Lösungsweg..
Vielen Dank schon im Voraus!
4 Antworten
Hallo.
Der Äquator ist der breiteste Teil der Erde, die Punkte, die auf dem Äquator liegen, sind eben genannte ~6370 Kilometer vom Erdmittelpunkt entfernt.
Mit der Formel U = 2π*r kannst du den Umfang der Erde bestimmen.
U = 2π*6370km
= 40.023km

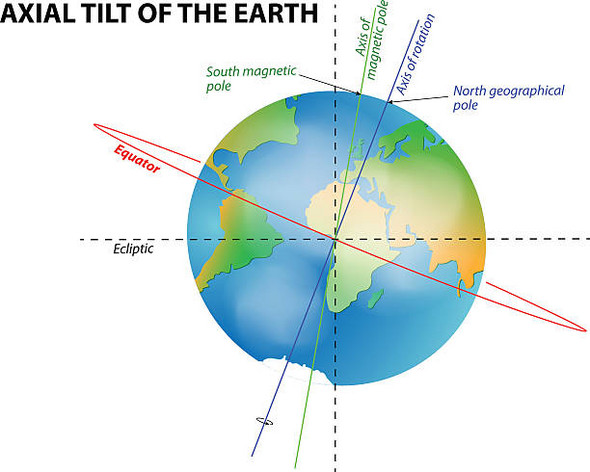
Der rote Kringel ist der Äquator. Orthogonal zum Äquator verläuft die Rotationsachse der Erde. Stell dir vor, wir nehmen den Punkt, an dem sich die beiden gestrichelten Linien kreuzen. Dieser dreht sich in 24h einmal um die Erde, entlang der roten Linie.
Jetzt weißt du, dass der Umfang der Erde ca. 40.023 km beträgt. Die Erde braucht 24h um sich einmal um sich selbst zu drehen, also wandert der Punkt in 24h 40.023 Kilometer weit (nämlich 1x um die Erde).
Dann nutzt du die Formel v = s/t um die Geschwindigkeit zu berechnen.
40.023km / 24h = 1667,6 km/h
Der Punkt bewegt sich also mit ca. 1668 km/h um den Erdmittelpunkt.
Diese Geschwindigkeit gilt aber nur dann, wenn du lediglich die Geschwindigkeit des Punktes in Abhängigkeit zum Erdmittelpunkt bestimmst. Da sich die Erde im All ja auch bewegt, wäre dieser Punkt in Abhängigkeit zur Sonne wesentlich schneller.
Für deine Aufgabe reicht aber die Antwort 1668 km/h.
Ich hoffe ich konnte dir helfen.
MfG
Lenny
Umfang ausrechnen, dann durch 24 Std. teilen, schon hast du Geschwindigkeit/Std. Fertig
Die Erde dreht sich in circa 24 Stunden um die eigene Achse. Davon geht man aus, sowie davon, dass der Erdradius circa 6370km beträgt.
Umfang der Erde = 2*Pi*Radius = 2*Pi*6370
Das ergibt eine Geschwindigkeit von 2*Pi*6370/24 km/h = 1667,6621km/h
Du brauchst den Umfang, nicht den Radius... du hast gerade berechnet wie schnell man sein müsste um innerhalb von 24h den Erdkern zu erreichen...
V=2*pi*r^2/T
Hier setzt du für r 6380000m ein und für T 24h in sekunden. Somit hast du V raus.
lG
r² bräuchtest du für die Fläche des Kreises (A = π*r²). Für den Umfang musst du nur 2π*r rechnen.
2 mal pi mal Radius, das durch 24