Baumdiagramm zeichnen und Wahrscheinlichkeit bestimmen?
Hallo zusammen, ich habe folgende Aufgabe:
in zwei kleinen Gummibären Packungen befinden sich je 5 rote und 3 grüne und 1 weißes Gummibärchen. aus jeder tüte wird ein Gummibärchen gezogen. zeichne ein passendes Baum Diagramm und beschrifte es vollständig.
Bestimme folgende Wahrscheinlichkeiten.
a= zwei weiße Bärchen
b= ein grüner und ein rotes Bärchen

Ich komme hier nicht weiter?
Kann mir jemand helfen?
f

2 Antworten
Hier kann man das vollständige Baumdiagramm doch noch zeichen:
Erste tüte (3 Verzweigungen) dann zweite (3 Verzweigungen), also 9 Enden.
Das sieht doch ganz gut aus. Du hast da doch 9 Enden. Jetzt musst du nur noch die passenden Pfade zu den gefragten Ereignissen heraussuchen und die Wahrscheinlichkeiten an den Enden addieren.
Du hast das Baumdiagramm doch richtig gezeichnet.
Und auch die passenden Wahrscheinlichkeiten der Ergebnisse hast du berechnet. Wobei aber...
Da hast du dich verrechnet.
Außerdem hast du dich bei der Ergebniswahrscheinlichkeit zum Ergebnis (G, R) nochmal anderweitig verrechnet. Da müsste eigentlich 5/9 ⋅ 3/9 statt 3/9 ⋅ 1/9 stehen.
Außerdem fehlt dir einmal bei 15/81 der Bruchstrich zwischen 15 und 81. Und sonst wäre es natürlich auch schön, wenn die äußere Form noch etwas sauberer wäre (bspw. Linien mit Lineal zeichnen).
Soweit aber schon einmal so gut. Bis auf ein paar Kleinigkeiten gar nicht mal so schlecht.
Jetzt fehlen dir noch die Wahrscheinlichkeiten zu den Ereignissen a und b.
- Weche Ergebnisse gehören denn zum Ereignis a „zwei weiße Bärchen dazu“? Addiere die entsprechenden Ergebniswahrscheinlichkeiten miteinander, um die gesuchte Wahrscheinlichkeit P(a) zu erhalten.
- Weche Ergebnisse gehören denn zum Ereignis b „ein grünes und ein rotes Bärchen“? Addiere die entsprechenden Ergebniswahrscheinlichkeiten miteinander, um die gesuchte Wahrscheinlichkeit P(b) zu erhalten.
Im konkreten Fall erhält man so...
- Zum Ereignis a gehört nur das Ergebnis (W, W). Es ist a = {(W, W)}. Dementsprechend erhält man...
- Zum Ereignis b gehören die Ergebnisse (G, R) und (R, G). Es ist b = {(G, R), (R, G)}. Dementsprechend erhält man...
====== Lösungsvorschlag zum Vergleich ======

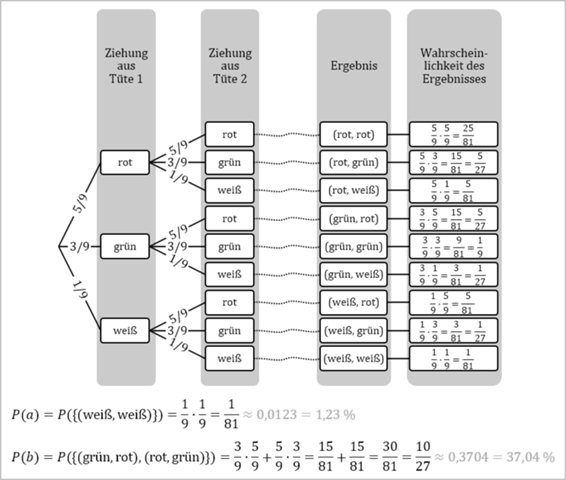
Danke, aber wieso 9 Enden. Ich verstehe das nicht. Habe einen Bild von meinem Versuch in der Frage gemacht. aber der ist sicherlich falsch. Kannst du mir weiterhelfen?