anfangswertprobleme?

Guten Abend, ich komme bei meiner Klausurvorbereitung nicht weiter. Könnte mir bitte jemand erklären, wie man die b) (untere Aufgabe) berechnet? Ich habe den Punkt in f‘ eingesetzt und für c 4 rausbekommen. Ich habe leider keine Ahnung, ob das der richtige Ansatz ist und wie ich weitermachen soll und würde mich deshalb sehr über Hilfe freuen! Liebe Grüße
3 Antworten
Guten Abend,
Lass erstmal f'(x) und f(x) darstellen:
f''(x) = 12x
f'(x) = 6x² + c
f(x) = 2x³ + cx + d
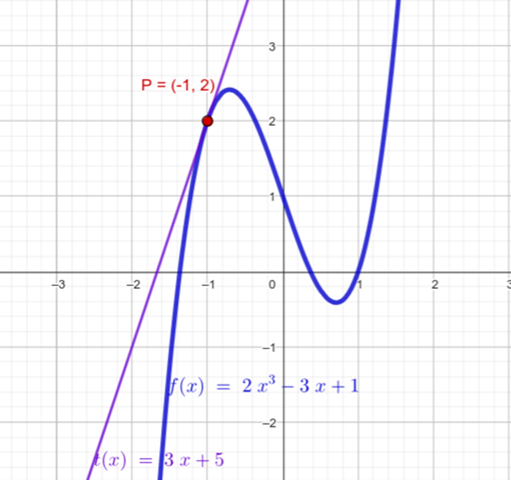
Wie man c berechnet: weil die steigung 3 ist, und f'(x) durch den Punkt (-1, 2) geht, ist f'(-1) = 3
3 = 6 * (-1)² + c
3 = 6 + c
c = -3
Wie man d berechnet: wenn man c berechnet hat, kann man einfach den Punkt (-1, 2) ausfüllen in f(x). Also
f(-1) = 2
f(x) = 2x³ - 3x + d
2 * (-1)³ - 3 * -1 + d = 2
-2 + 3 + d = 2
d = 1
Also f(x) = 2x³ - 3x + 1
Mit freundlichen Grüßen
Tijn
f´´(x) = 12 * x
f´(x) = 6 * x ^ 2 + b
f(x) = 2 * x ^ 3 + b * x + c
f(-1) = 2 , daraus folgt:
2 * (-1) ^ 3 - b * 1 + c = 2
Vereinfachen:
- b + c = 4
f´(-1) = 3, daraus folgt:
6 * (-1) ^ 2 + b = 3
Vereinfachen:
b = -3
Daraus folgt:
- (-3) + c = 4
c = 1
Fazit:
f(x) = 2 * x ^ 3 - 3 * x + 1
Da bei b) die 2. Ableitung steht:
Mit m=3 im Punkt P(-1|2) gelten die Bedingungen:
Skizze